爱刨根知识网

  1. 首页 > 经验知识 > >

如何证明勾股定理的逆定理，勾股定理的逆定理教学视频

生活经验勾股定理

如何证明勾股定理的逆定理
先假设一个直角三角形，然后使其两直角边与三角形ABC的两条较短边相等，之后既可得这两个三角形全等（SAS），既三角形ABC为直角三角形 。
勾股定律又称勾股弦定理、勾股定理，是一个基本的几何定理，指直角三角形的两条直角边长（古称勾长、股长）的平方和等于斜边长（古称弦长）的平方 。
勾股定理的逆定理教学视频勾股定理的逆定理是，如果一个三角形两直角边的平方和等于斜边的平方，那么这个三角形是直角三角形 。
勾股定理的逆定理是判断三角形为钝角、锐角或直角的一个简单的方法，其中AB=c为最长边 。
如果a2 + b2 = c2 ，则△ABC是直角三角形 。
如果a2 + b2 > c2 ，则△ABC是锐角三角形（若无先前条件AB=c为最长边，则该式的成立仅满足∠C是锐角） 。
如果a2 + b2

如何证明勾股定理的逆定理，勾股定理的逆定理教学视频

文章插图
勾股定理的具体解释如下：
1、勾股定理（Pythagorean theorem）又称商高定理、毕达哥拉斯定理、毕氏定理、百牛定理，是平面几何中一个基本而重要的定理 。勾股定理是人类早期发现并证明的重要数学定理之一 。
2、勾股定理说明，平面上的直角三角形的两条直角边的长度（古称勾长、股长）的平方和等于斜边长（古称弦长）的平方 。
3、反之，若平面上三角形中两边长的平方和等于第三边边长的平方，则它是直角三角形（直角所对的边是第三边） 。
如何证明勾股定理的逆定理成立正弦定理证明方法
方法1:用三角形外接圆
证明： 任意三角形ABC,作ABC的外接圆O.
作直径BD交⊙O于D. 连接DA.
因为直径所对的圆周角是直角,所以∠DAB=90度
因为同弧所对的圆周角相等,所以∠D等于∠C. 所以c/sinC=c/sinD=BD=2R
类似可证其余两个等式 。
∴a/sinA=b/sinB=c/sinC=2R
方法2: 用直角三角形
证明：在锐角△ABC中，设BC=a,AC=b,AB=c 。作CH⊥AB垂足为点H
CH=a·sinB CH=b·sinA ∴a·sinB=b·sinA 得到a/sinA=b/sinB
同理，在△ABC中， b/sinB=c/sinC ∴a/sinA=b/sinB=c/sinC
在直角三角形中,在钝角三角形中(略) 。
方法3：用向量
证明：记向量i ，使i垂直于AC于C，△ABC三边AB,BC,CA为向量a,b,c ∴a+b+c=0 则i(a+b+c) =i·a+i·b+i·c
=a·cos(180-(C-90))+0+c·cos(90-A)=-asinC+csinA=0 ∴a/sinA =c/sinC (b与i垂直,i·b=0)
方法4：用三角形面积公式
证明：在△ABC中，设BC=a,AC=b,AB=c 。作CD⊥AB垂足为点D，作BE⊥AC垂足为点E，则CD=a·sinB，BE= c sinA,由三角形面积公式得：AB·CD=AC·BE
即c·a·sinB= b·c sinA ∴a/sinA=b/sinB 同理可得b/sinB=c/sinC
∴a/sinA=b/sinB=c/sinC
勾股定理逆定理怎么证明的勾股定理：a2+b2=c2
如果知道a或b的平方，就可以用a或b加一个小数字来尝试
知道c的长度，就把它拆成两个和比自己大的数字来验证
勾股定理
如果直角三角形两直角边分别为A，B，斜边为C，那么 A^2+B^2=C^2;； 即直角三角形两直角边长的平方和等于斜边长的平方 。如果三角形的三条边A，B，C满足A^2+B^2=C^2;，还有变形公式：
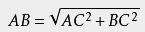
如何证明勾股定理的逆定理，勾股定理的逆定理教学视频

文章插图
，如：一条直角边是a，另一条直角边是b，如果a的平方与b的平方和等于斜边c的平方那么这个三角形是直角三角形 。（称勾股定理的逆定理）
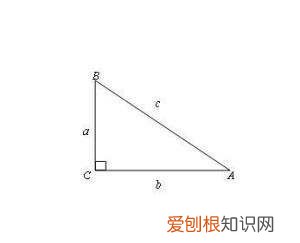
如何证明勾股定理的逆定理，勾股定理的逆定理教学视频

文章插图
直角三角形由 毕达哥拉斯在公元前550年提出 。
【如何证明勾股定理的逆定理，勾股定理的逆定理教学视频】

推荐阅读


上一篇：农村封闭式化粪池的污水怎么处理 化粪池多久清理一次

下一篇：Windows xp系统增加虚拟内存加快运行速度的两种方法