对于像爱因斯坦那样超前自学的人 , 学校的作用无疑是大大弱化 , 甚至往往只会显出羁绊的 , 但如果被爱因斯坦大力“点赞”的“神圣的几何学小书”是路特波德中学的教本 , 路特波德中学总也该分到一些功劳吧 。更何况那个教本的作者阿道夫西肯伯格 (Adolf Sickenberger) 也正是路特波德中学的教师 。将这些因素综合起来 , 我觉得也许可以这样来评价路特波德中学:爱因斯坦对教育体制——尤其是对当时德国的教育体制——的批评无疑有着深刻的一面 , 但如果因为他这个“非典型性”学生在很多年之后所表述的个人评价 , 就将路特波德中学视为一间特别糟糕的学校 , 抹杀其在教材和教师方面的出色之处 , 那是不公允的 。
既然说到了“神圣的几何学小书” , 不能不顺便提一下爱因斯坦童年时代跟几何的另一次“亲密接触” 。依据晚年自述 , 这次接触发生在他得到“神圣的几何学小书”之前 , 是来自他的叔叔雅各布爱因斯坦 (Jakob Einstein)。雅各布是一位对爱因斯坦的智力发展产生过重大影响的叔叔 。除几何外 , 这位叔叔对“代数”的一句风趣介绍也是爱因斯坦津津乐道的——而且拿到今天也不失高明 , 甚至被认为对爱因斯坦本人的“科普”风格有过影响 。雅各布说 , 代数是“一门愉快的科学 , 当我们想抓的动物没被抓到时 , 我们暂时称它为x , 然后继续抓捕直到它落网 。”回到几何上来 , 雅各布将毕达哥拉斯定理 (Pythagorean theorem) 告诉了爱因斯坦(但未予证明) , 使后者大为着迷 , 并在“经过很多努力”之后证明了这个定理 。
学过几何的读者都知道 , 几何的证明——乃至其他数学证明——是要从公理、定义等等出发的 , 从而离不开某种体系 。爱因斯坦既然尚未学过“神圣的几何学小书” , 他是怎样证明毕达哥拉斯定理的呢?这个有趣的问题虽无第一手的答案 , 但依据爱因斯坦留下的片言只语的线索 , 人们已能很有把握地复现他的证明 。在晚年自述中 , 爱因斯坦提供了一条线索:即他的证明用到了直角三角形的“相似性”(考虑到他当时尚未学过几何 , 这一术语当是回忆时的借用) 。具体地说 , 他认为足够显然——从而可作为证明依据的是:“直角三角形各边的关系完全取决于它的一个锐角”(换句话说 , 两个直角三角形若有一个锐角相同 , 则彼此“相似”) 。另一条线索则出现在波兰哲学家亚历山大莫兹科夫斯基 (Alexander Moszkowski) 1921年出版的Einstein The Searcher : His Work Explained From Dialogues With Einstein(《探索者爱因斯坦:通过与爱因斯坦的对话解读他的工作》)一书中 。莫兹科夫斯基是爱因斯坦的朋友 , 他这本书记录了与爱因斯坦的很多对话及来自对话的信息 , 其中提到爱因斯坦在证明中作了一条从直角三角形的直角顶点到对边的垂线 。
文章插图
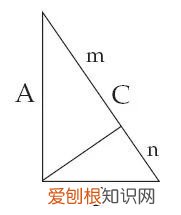
依据这两条线索便可以很有把握地复现爱因斯坦的证明 。上图画出了一个直角三角形及从直角顶点到对边的垂线 , 并对各线段作了标注:A、B、C是直角三角形三条边的长度 , m、n为斜边被垂线分成的两个线段的长度 。显然 , 图中的两个小直角三角形分别跟大直角三角形共享一个锐角 , 从而“各边的关系”完全相同 。因此:A/C=m/A , B/C=n/B;略微变形后可得:A^2=mC , B^2=nC , 因此A^2+B^2=(m+n)C=C^2 。证毕 。这个证明用到了爱因斯坦给出的两条线索 , 且只用到了那两条线索 , 故极有可能就是爱因斯坦的证明 。虽尚未读过“神圣的几何学小书” , 证明毕达哥拉斯定理的这一努力还是让童年爱因斯坦领会到了数学证明的一个重要特点 , 那就是“只有……不‘显然’的东西才需要证明” 。有了这种领会 , 当他读到“神圣的几何学小书”时 , 对公理的存在及必须不加证明地接受公理这一特点就并不觉得困扰了 。
推荐阅读
- 在家学做醋泡鸡蛋 米醋泡鸡蛋
- ICU到底是一个什么科室? 什么是icu病房
- 气质唯美的韩式新娘盘发 新娘韩式盘发
- 考试心态调整及应试策略 考试心理
- 潜水艇鱼怎么养 饲养的时候需要加盐 潜水艇鱼怎么养
- 泡茶的基本步骤! 冲茶步骤!
- 大北农股票目标价是多少_大北农集团最新消息
- 北面后面的帽子怎么收 - 北面1996帽子怎么收纳
- LA柜号是什么船公司 - 船公司价格不出就不能装柜吗


