平面束方程怎么用，过某直线的平面束方程怎么求

平面束方程怎么用
平面束的概念及其方程是空间解析几何中的一个重要工具，在很多问题中如果使用平面束的方法会使问题简化，例如求直线在某平面上的投影、以及异面直线的相关问题。
例如：高等数学点法式求平面束方程如x+3/2=y-5/3=z/1求出平面束方程。
x+3-z+λ(y-5-3z)=0
你由平面束的定义来：
设直线L由方程组：A1X+B1Y+C1Z+D1=0;
A2X+B2Y+C3Z+D2=0所确定
我们就建立：A1X+B1Y+C1Z+D1+λ（A2X+B2Y+C3Z+D2）=0这就表示一个平面。
这题与之对应：平面方程组：x+3/2=z/1①
y-5/3=z/1②所确定就成了我给的结果
（注：你也可以任意取两个：x+3/2=y-5/3
y-5/3=z/1也是正确的）。
过某直线的平面束方程怎么求过直线的平面束方程: λ(x+5y+z)+μ(x-z+4)=0 (λ+μ)x+5λy+(λ-μ)z+4μ=0
通过空间直线L的平面有无穷多个，将通过空间直线L的所有平面的集合称为过直线L的的平面束，设直线L的一般式方程为

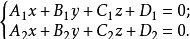
文章插图
其中系数不成比例，构造一个三元一次方程：

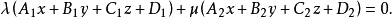
文章插图
则上式可写成

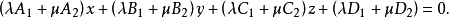
文章插图
由于系数与不成比例，所以，上述方程的一次项系数不全为零，从而它表示一个平面，对于不同的
系数值，所对应的平面也不同，而且这些平面都通过直线L，也就是说，这个方程表示通过直线L的一族平面，另一方面，任何通过直线L的平面也一定包含在上述通过L的平面族中，因此，上述方程

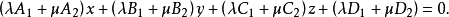
文章插图
就是通过直线L的平面束方程。
代入数值得过直线的平面束方程是 λ(x+5y+z)+μ(x-z+4)=0 (λ+μ)x+5λy+(λ-μ)z+4μ=0

文章插图
扩展资料
平面束属于一种空间图形，是一组有特殊位置关系的平面的集合，即有一条公共直线的所有平面的集合。平面束指如下的两种平面集合：1.由所有彼此平行的平面组成的集合称为平行平面束；2.由相交于同一条直线的所有平面组成的集合称为共线平面束、有轴平面束或相交平面束，这条直线称为共线平面束的轴。
参考资料
怎么通过直线x-45=y+32=z的平面束方程方法1：
设平面束π为： A(x － x0) + B(y － y0) + C(z － z0) ＝ 0
因为平面束π通过直线L，可以取点P0（x0，y0，z0）为直线上特殊点（4, －3 0）
则平面束π为： A(x － 4) + B(y ＋ 3) + Cz ＝ 0
又直线L的方向相量（5，2，1）与平面束π的法向量（A，B，C）垂直，则
（A，B，C） * （5，2，1）＝0
即5A + 2B + C＝0
假定A ＝ 2μ B＝5λ 则 C＝－10μ － 10λ
所以平面束π为： 2μ(x － 4) + 5λ(y + 3) －10(μ + λ)z ＝ 0
经整理得平面束π为： μ(2x － 10z - 4) + λ(5y -10z + 15) ＝ 0 ①
方法2：直线（x-4）/5 =（y+3）/2 = z/1
即 x - 4 = 5z
y + 3 = 2z
所以平面束π为： μ(x - 5z + 4) + λ( y - 2z + 3) ＝ 0 ②
总结，希望对你学习有些用处：
1、①和②的区别在于，两个系数之间有一个倍数关系.
2、方法1先假设了平面束方程，然后逐步确定系数和参数；
3、方法2先用直线的标准式（点法式、对称式）转化为一般式，然后构造平面束方程；
4、平面束一般取完整的形式： μ (F1方程) + λ (F2方程) ＝ 0 其中μλ不同时为0；
有时候为了方便忽略F2方程，取为： F1方程 + λ (F2方程) ＝ 0 不包括F2方程平面；

平面束方程怎么用，过某直线的平面束方程怎么求

推荐阅读

关于节约粮食的名言诗句关于节约粮食的名言和诗句

奋斗励志朋友圈句子励志短句致自己奋斗朋友圈

想发朋友圈表示心情不好的句子心情不好发朋友圈的句子心情短句

贝拉玻尿酸是合法的吗贝拉玻尿酸是进口的还是国产的

核桃仁做菜的菜谱，您知道桃仁脆溜鸡的做法

浅紫色显皮肤黑还是白

库伦旗景点

居家隔离和集中隔离的区别什么情况下要隔离28天

蝉蛹是什么

怎样能丰胸最安全有效