正四面体是什么，什么是正四面体

正四面体是什么
正四面体是由四个全等正三角形围成的空间封闭图形，所有棱长都相等。它有4个面，6条棱，4个顶点。正四面体是最简单的正多面体。正四面体是五种正多面体中的一种，有4个正三角形的面，4个顶点，6条棱。正四面体不同于其它四种正多面体，它没有对称中心。
正四面体有六个对称面，其中每一个都通过其一条棱和与这条棱相对的棱的中点。正四面体很容易由正方体得到，只要从正方体一个顶点A引三个面的对角线AB，AC，AD，并两点两点连结之即可。正四面体和一般四面体一样，根据保利克-施瓦兹定理能够用空间四边形及其对角线表示。正四面体的对偶是其自身。
正四面体的性质
1、正四面体的每一个面是正三角形，反之亦然。
2、正四面体是三组对棱都垂直的等面四面体。
3、正四面体是两组对棱垂直的等面四面体。
4、正四面体的各棱的中点是正八面体的六顶点。
5、正四面体的四个旁切球半径均相等，等于内切球半径的2倍，或等于四面体高线的一半。
什么是正四面体正四面体是：是由4个等边三角形围成的封闭的体形，它有4个面，每个面都是等边三角形，有6个相等的棱，有4个顶点
正四面体是什么正四面体是由四个全等正三角形围成的空间封闭图形，所有棱长都相等。它有4个面，6条棱，4个顶点。正四面体是最简单的正多面体。正四面体是五种正多面体中的一种，有4个正三角形的面，4个顶点，6条棱。正四面体不同于其它四种正多面体，它没有对称中心。
正四面体有六个对称面，其中每一个都通过其一条棱和与这条棱相对的棱的中点。正四面体很容易由正方体得到，只要从正方体一个顶点A引三个面的对角线AB，AC，AD，并两点两点连结之即可。正四面体和一般四面体一样，根据保利克-施瓦兹定理能够用空间四边形及其对角线表示。正四面体的对偶是其自身。
正四面体的性质
1.正四面体的每一个面是正三角形，反之亦然。
2.正四面体是三组对棱都垂直的等面四面体。
3.正四面体是两组对棱垂直的等面四面体。
4.正四面体的各棱的中点是正八面体的六顶点。
5.正四面体的四个旁切球半径均相等，等于内切球半径的2倍，或等于四面体高线的一半。
什么是正四面体空隙正四面体是由四个等边三角形组成的正多面体，也是一个正三棱锥，有4个顶点和6条边
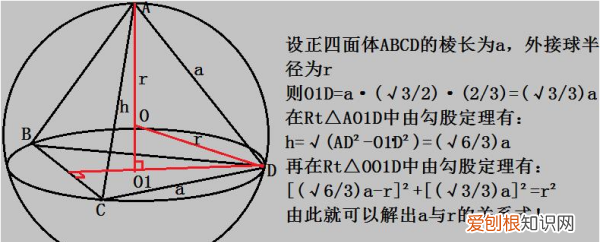
什么是正四面体1、外接球。
边长为a的正四面体可以看成是边长是（√2/2）a的正方体截出来的，则其外接球直径是正方体边长的√3倍。
2、内切球半径。
设正四面体是S－ABC，过点S作高线SH交底面ABC于点H，则内切球球心在SH上，设其半径是R，则主要就产生四个四面体：O－SAB、O－SBC、O－SCA、O－ABC，这四个四面体的高都是内切球的半径R，底面都是以a为边长是正三角形，利用等体积法可以求出内切球半径R的值。

文章插图
四面体为正四面体的充要条件是
其棱均做为外接平行六面体的侧面对角线时，平行六面体为正方体。
四面体为正四面体的充要条件是，其共顶点三i棱作为外接平行六面体的棱时，平行六面体为一个三面角面角均为60°的菱形六面体。
四面体为正四体的充要条件是，四面体在平行于两棱的每一个平面的射影是正方形。
四面体为正四面体的充要条件是，四面体的展开图是一个引出了三条中位线的正三角形。
正四面体每条高的中点与底面三角形三顶点均构成直角四面体的四顶点，且高的中点为址三面角顶点。

正四面体是什么，什么是正四面体

推荐阅读

关于节约粮食的名言诗句关于节约粮食的名言和诗句

奋斗励志朋友圈句子励志短句致自己奋斗朋友圈

想发朋友圈表示心情不好的句子心情不好发朋友圈的句子心情短句

贝拉玻尿酸是合法的吗贝拉玻尿酸是进口的还是国产的

核桃仁做菜的菜谱，您知道桃仁脆溜鸡的做法

浅紫色显皮肤黑还是白

库伦旗景点

居家隔离和集中隔离的区别什么情况下要隔离28天

蝉蛹是什么

怎样能丰胸最安全有效