第一类间断点包含哪些，高等数学中的符号表示大全

第一类间断点包含哪些
第一类间断点包含可去间断点和跳跃间断点，在第一类间断点中，有两种情况，左右极限存在是前提。左右极限相等，但不等于该点函数值f(x0)或者该点无定义时，称为可去间断点，如函数y=（x2-1)/(x-1)在点x=1处；左右极限在该点不相等时，称为跳跃间断点，如函数y=|x|/x在x=0处。
设函数y=f(x)在点x0的某一去心邻域内有定义，如果函数f(x)当x→x0时的极限存在，且等于它在点x0处的函数值f(x0) ，即limf(x)=f(x0)（x→x0），那么就称函数f(x)在点x0处连续。
不连续情形：
1、在点x=x0没有定义；
2、虽在x=x0有定义但lim（x→x0）f(x)不存在；
3、虽在x=x0有定义且limf(x)（x→x0）存在，但limf(x)≠f(x0)（x→x0）时则称函数在x0处不连续或间断。
高等数学中的符号表示大全第一类间断点：1.可去间断点：若limf(x)=A(X趋近于X0时)但A不等于x0时或f(x0)无定义。2.跳跃间断点：若limf(x)（X→Xο－)与limf(x)（X→Xο+)都存在但不相等.
第二类间断点:若limf(x)（X→Xο－)与limf(x)（X→Xο+)至少有一个不存在,则Xο点为第二类间断点.
函数的间断点分为几类?第一类间断点（左右极限都存在）有以下两种
1跳跃间断点间断点两侧函数的极限不相等
【第一类间断点包含哪些，高等数学中的符号表示大全】2可去间断点间断点两侧函数的极限存在且相等函数在该点无意义
第二类间断点（非第一类间断点）也有两种
1振荡间断点函数在该点处在某两个值比如-1和+1之间来回振荡
2无穷间断点函数在该点极限不存在趋于无穷
间断点分几个类型?判定标准是什么?间断点类型是：可去间断点，跳跃间断点等。
间断点的分类及判断方法：
用左右极限判断是第一类间断点还是第二类间断点，第一类间断点包括第一类可去间断点和第一类不可去间断点，如果该点左右极限都存在，则是第一类间断点。
其中如果左右极限相等，则是第一类可去间断点，如果左右极限不相等，则是第一类不可去间断点，即第一类跳跃间断点。如果左右极限中有一个不存在，则第二类间断点。
间断点可以分为无穷间断点和非无穷间断点，在非无穷间断点中，还分可去间断点和跳跃间断点。如果极限存在就是可去间断点，不存在就是跳跃间断点。

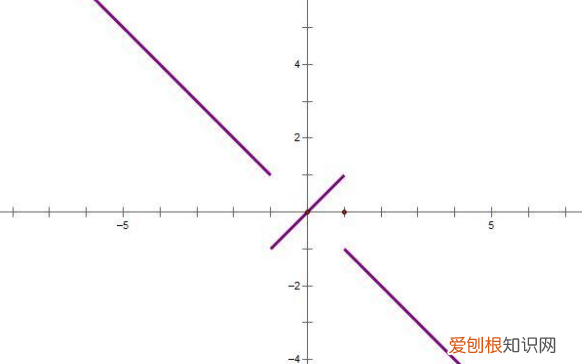
文章插图
间断点简介：
间断点是指：在非连续函数y=f(x)中某点处xo处有中断现象，那么， xo就称为函数的不连续点。
间断点可以分为无穷间断点和非无穷间断点，在非无穷间断点中，还分可去间断点和跳跃间断点。如果极限存在就是可去间断点，不存在就是跳跃间断点。
只有有限个第一类间断点是什么意思第一类间断点就是左右极限都存在的间断点，如左右极限相等时，即极限存在时的间断点称之为可去间断点，如左右极限不相等的间断点称之为跳跃间断点。
左右极限至少有一个不存在时，称此间断点为第二类间断点，左右极限中有一个为无穷大时，称此间断点为无穷远间断点，当函数有界时，称此第二类间断点为振荡间断点。

第一类间断点包含哪些，高等数学中的符号表示大全

推荐阅读

关于节约粮食的名言诗句关于节约粮食的名言和诗句

奋斗励志朋友圈句子励志短句致自己奋斗朋友圈

想发朋友圈表示心情不好的句子心情不好发朋友圈的句子心情短句

贝拉玻尿酸是合法的吗贝拉玻尿酸是进口的还是国产的

核桃仁做菜的菜谱，您知道桃仁脆溜鸡的做法

浅紫色显皮肤黑还是白

库伦旗景点

居家隔离和集中隔离的区别什么情况下要隔离28天

蝉蛹是什么

怎样能丰胸最安全有效