导数存在的充要条件
导数存在的充要条件是左导数=右导数 。
一个函数在某点连续,表明它在该点左右极限相等zhi且等于该点的函数值.对导函数z说,导函数连续意味着f'(x)在x0的左右极限相等且等于f'(x0) 。
如果函数f(x)在(a,b)中每一点处都可导,则称f(x)在(a,b)上可导,则可建立f(x)的导函数,简称导数,记为f'(x) 。
如果f(x)在(a,b)内可导,且在区间端点a处的右导数和端点b处的左导数都存在,则称f(x)在闭区间[a,b]上可导,f'(x)为区间[a,b]上的导函数,简称导数 。
若将一点扩展成函数f(x)在其定义域包含的某开区间I内每一个点,那么函数f(x)在开区间内可导,这时对于内每一个确定的值,都对应着f(x)的一个确定的导数,如此一每一个导数就构成了一个新的函数,这个函数称作原函数f(x)的导函数,记作:y'或者f′(x) 。
函数在某点处可导的充要条件是什么?函数在某点可导的充分必要条件:某点的左导数与右导数存在且相等 。
判断不可导:
1、证明左导数不等于右导数
2、证明左导数或者右导数不存在(无穷大或者不可取值)
例如:
f(x)=x的绝对值,但当x<0时,f(x)的导数等于-1,当x>0是,f(x)的导数等于1 。
不相等,所以在x=0处不可导 。
文章插图
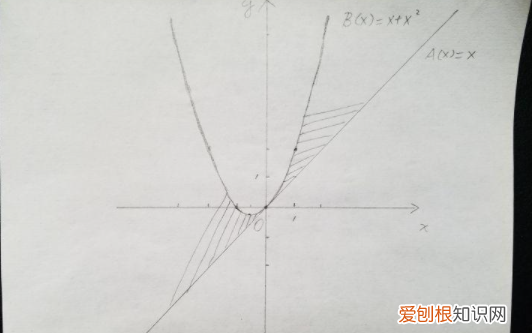
可导函数、不可导函数和物理、几何、代数的关系:
导数与物理、几何和代数关系密切:在几何中可以求正切;在代数中可以求瞬时变化率;在物理中可以求速度和加速度 。物理学、几何学、经济学等学科中的一些重要概念可以用导数来表示 。
例如,导数可以表示运动物体的瞬时速度和加速度(对于线性运动,位移的一阶导数是相对于时间的瞬时速度,二阶导数是加速度),曲线在一点的斜率,以及经济学中的边际和弹性 。
导数存在的充分条件1/h趋于0如果一个函数可导,其必然连续 。如果一个函数连续,则不一定可导 。如y=lxl
函数在一点可导的充分必要条件是连续的函数,在该点的左右极限存在且相等 。
当然,同济课本上这么说过,函数可导的充要条件是左导数和右导数相等,这是一个意思 。
至于函数的一致连续性,这个不常用只是个概念问题,我没有听说过他和可导的关系,它的概念我记不清了,不过不论是学习还是考研,重点还是你前一部分说的连续,可导,还有一个是极限 。
复函数可导的充要条件是什么关于函数的可导导数和连续的关系:
1、连续的函数不一定可导 。
2、可导的函数是连续的函数 。
3、越是高阶可导函数曲线越是光滑 。
4、存在处处连续但处处不可导的函数 。
左导数和右导数存在且“相等”,才是函数在该点可导的充要条件,不是左极限=右极限(左右极限都存在) 。连续是函数的取值,可导是函数的变化率,当然可导是更高一个层次 。
函数在某点可导的充要条件是左右导数相等且在该点连续 。显然,如果函数在区间内存在“折点”,(如f(x)=|x|的x=0点)则函数在该点不可导 。
向左转|向右转
文章插图
函数在某点处可导的充分必要条件是什么函数在某一点可导的充分必要条件有满足导数定义
、可微
、左右导数存在且相等 。函数在某一点导函数连续的充分必要条件就是导函数作为函数时连续的充分必要条件 。
【扩展资料】
【导数存在的充要条件,函数在某点处可导的充要条件是什么?】
推荐阅读
- 硬笔怎样执笔,写硬笔字的正确执笔姿势是什么样的
- 2021年9月新能源车销量排行榜 新能源车销售排行榜前十名9月
- 两个白羊座女生能和平相处吗? 最难相处星座排行榜大全女生
- 70年代创业励志电视剧大全排名榜? 励志创业电视剧排行榜大全
- 苹果怎么设置壁纸,苹果手机怎么设置壁纸
- excel自动减怎么用
- 抖音用qq登录未获得权限,抖音怎么用qq登录未授权怎么办
- 炒茶叶怎么炒
- win0控制面板在哪里,nvidia控制面板在哪里打开


