无穷间断点是第二类间断点吗
对的 。
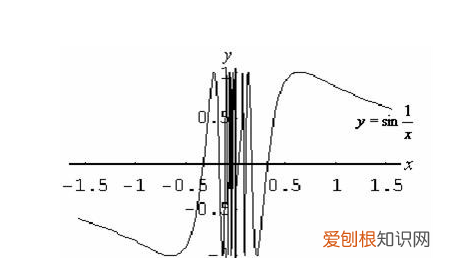
第二类间断点是指函数的左右极限至少有一个不存在 。第二类间断点有非常多种,如无穷间断点,振荡间断点,单侧间断点,狄利克雷函数间断点等等 。当x趋向于x0时,f(x)趋向于无穷大,故x=x0为无穷间断点 。
间断点是指:在非连续函数y=f(x)中某点处xo处有中断现象,那么,xo就称为函数的不连续点 。间断点可以分为无穷间断点和非无穷间断点,在非无穷间断点中,还分可去间断点和跳跃间断点 。
第二类间断点怎么判断原函数第二类间断点:
函数的左右极限至少有一个不存在 。a若函数在x=Xo处的左极限或右极限至少有一个为无穷大,则称x=Xo为f(x)的无穷间断点 。例y=tanx,x=π/2 。
b若函数在x=Xo处的左右极限都不存在且非无穷大,则称x=Xo为f(x)的振荡间断点 。
首先讲一下间断点的类型,有第一类间断点:其中包括可去间断点(左右极限相等此点无意义)、跳跃间断点(左右极限不相等) 。
第二类间断点:震动间断点(函数值在上下来回震动)、无限间断点(函数值)判断方法首先找出函数没有意义的点 。
文章插图
相关计算:
设Xo是函数f(x)的间断点,那么如果f(x-)与f(x+)都存在,则称Xo为f(x)的第一类间断点 。又如果(i),f(x-)=f(x+)≠f(x),或f(x)无意义,则称Xo为f(x)的可去间断点 。
(ii),f(x-)≠f(x+),则称Xo为f(x)的跳跃间断点 。
间断点类型有哪些第一类间断点(左右极限都存在)有以下两种 :
1、跳跃间断点,间断点两侧函数的极限不相等 。
2、可去间断点,间断点两侧函数的极限存在且相等,函数在该点无意义 。
第二类间断点(非第一类间断点)也有两种 :
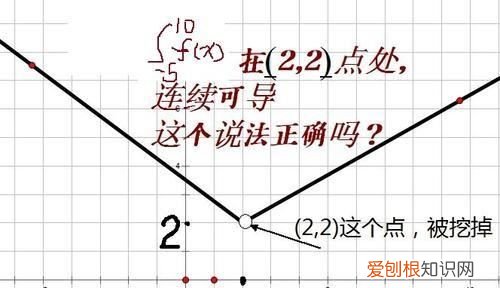
1、振荡间断点,函数在该点处在某两个值比如-1和+1之间来回振荡 。
2、无穷间断点,函数在该点极限不存在趋于无穷先看函数在哪些点是没有意义的再分两大类判断无穷间断点 和 非无穷间断点这两种应该很容易区分在 非无穷间断点 中,还分可去间断点和跳跃间断点如果极限存在就是可去间断点,不存在就是跳跃间断点 。
文章插图
扩展资料
间断点的分类也按极限的情况来分:左、右极限都存在的间断点称第一类间断点(包括可去间断点和跳跃间断点两种)左右极限至少有一个不存在的间断点称为 第二类间断点(包括无穷间断点,振荡间断点,以及其它有名称或无名称的间断点) 。
此外,在双侧极限无意义而单侧极限有意义时,也按单侧极限存在与否来对间断点分类 。连续函数的图像是一条连绵不断的曲线,判断函数在某点是否连续,也就是看该点的极限是否等于该点函数值,即,若相等则连续 。同理,不连续就是间断,也就是说,若破坏了连续的条件,函数在该点就间断不连续 。
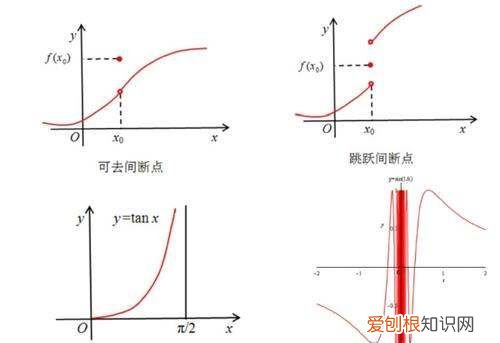
间断点有哪几类类型左右极限存在且相等的间断点,叫可去间断点 。
左右极限存在且不相等的间断点,叫跳跃间断点 。
左右极限为无穷的间断点,叫做无穷间断点,其中无穷是个可以解出的答案,但一般视为极限不存在 。
左右极限振荡不存在的间断点,叫做振荡间断点,其中振荡是不可以解出的答案,极限完全不存在 。
文章插图
扩展资料:
举例说明:
设x1是某函数的间断点 。
1、第一类间断点包括:可去间断点和跳跃间断点 。
①可去间断点左右极限存在且相等,但不等于f(x1),如y=x2—1/x—1,x=1为x的可去间断点 。从图像上看,只要在x1处添上一点y=limf(x),整个图像就是连续的曲线 。x ?x1
推荐阅读
- 桌面快捷方式怎么设置,怎样在电脑桌面添加程序的快捷方式
- 小米手机导航键怎么设置出来,小米手机怎么切换成经典导航键
- 杜甫的望岳是哪座山
- 经济学专业好找工作吗 经济学包括哪些专业
- 孜然粒多少钱一斤?,孜然粒大约多少钱一斤
- 标准布朗运动的性质 标准布朗运动
- 成都限号规定区域 成都限号规定
- 快手买东西在哪里找 快手商城在哪里能找到
- 神奇的“梅花易数” 梅花易数断寿命


