期望与方差的关系，二项分布的期望和方差是什么意思

期望与方差的关系
方差=E(x2)-E(x)2，E(X)是数学期望。在概率论和统计学中，数学期望(mean)（或均值，亦简称期望）是试验中每次可能结果的概率乘以其结果的总和，是最基本的数学特征之一。它反映随机变量平均取值的大小。
方差在概率论和统计学中，一个随机变量的方差描述的是它的离散程度，也就是该变量离其期望值的距离。一个实随机变量的方差也称为它的二阶矩或二阶中心动差，恰巧也是它的二阶累积量。这就是将各个误差将之平方，相加之后再除以总数，透过这样的方式来算出各个数据分布、零散的程度。
二项分布的期望和方差是什么意思六个常见分布的期望和方差：
1、均匀分布，期望是（a+b）/2，方差是（b-a）的平方/12 。
2、二项分布，期望是np，方差是npq 。
3、泊松分布，期望是p，方差是p 。
4、指数分布，期望是1/p,方差是1/(p的平方) 。
5、正态分布，期望是u，方差是&的平方。
6、x服从参数为p的0-1分布，则e(x)=p，d(x)=p(1-p) 。

文章插图
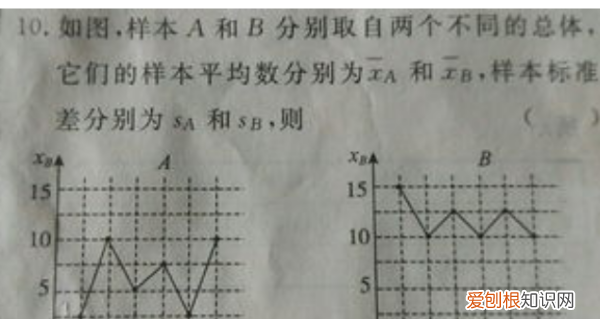
二项分布：
在每次试验中只有两种可能的结果，而且两种结果发生与否互相对立，并且相互独立，与其它各次试验结果无关，事件发生与否的概率在每一次独立试验中都保持不变，则这一系列试验总称为n重伯努利实验，当试验次数为1时，二项分布服从0-1分布。
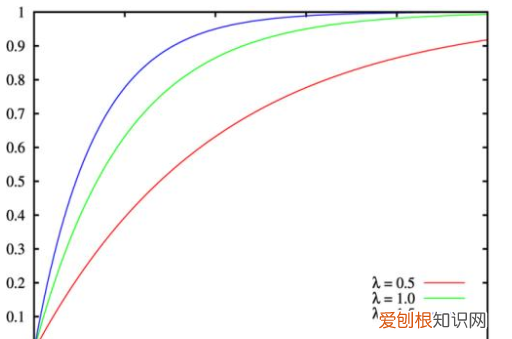
指数分布的期望和方差有什么关系指数分布的期望：E（X）=1/λ 。
指数分布的方差：D（X）=Var（X）=1/λ2 。
指数分布与分布指数族的分类不同，后者是包含指数分布作为其成员之一的大类概率分布，也包括正态分布，二项分布，伽马分布，泊松分布等等。

文章插图
六个常见分布的期望和方差：
1、均匀分布，期望是（a+b）/2，方差是（b-a）的平方/12 。
2、二项分布，期望是np，方差是npq 。
3、泊松分布，期望是p，方差是p 。
4、指数分布，期望是1/p,方差是1/(p的平方) 。
5、正态分布，期望是u，方差是&的平方。
6、x服从参数为p的0-1分布，则e(x)=p，d(x)=p(1-p) 。
方差与数学期望之间的公式为D(X)=E{[X-E[X]]^2}
=E{X^2-2*X*E[X]+E[X]^2}
=E[X^2]-E{2*X*E[X]}+E{E[X]^2}
=E[X^2]-2*E[X]*E[X]+E[X]^2
=X[X^2]-E[X]^2
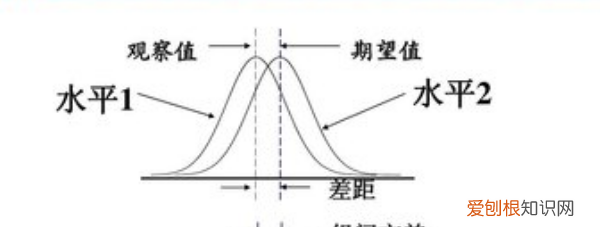
概率论中方差用来度量随机变量和其数学期望（即均值）之间的偏离程度。统计中的方差（样本方差）是每个样本值与全体样本值的平均数之差的平方值的平均数。在许多实际问题中，研究方差即偏离程度有着重要意义。

文章插图
扩展资料：
离散型随机变量与连续型随机变量都是由随机变量取值范围(取值)确定。
变量取值只能取离散型的自然数，就是离散型随机变量。例如，一次掷20个硬币，k个硬币正面朝上，k是随机变量。k的取值只能是自然数0，1，2，?，20，而不能取小数3.5，因而k是离散型随机变量。
如果变量可以在某个区间内取任一实数，即变量的取值可以是连续的，这随机变量就称为连续型随机变量。例如，公共汽车每15分钟一班，某人在站台等车时间x是个随机变量，x的取值范围是[0,15），它是一个区间，从理论上说在这个区间内可取任一实数3.5，因而称这随机变量是连续型随机变量。
方差和期望的关系公式推导方差和期望的关系公式：DX=EX^2-(EX)^2 。若随机变量X的分布函数F(x)可表示成一个非负可积函数f(x)的积分，则称X为连续性随机变量，f(x)称为X的概率密度函数（分布密度函数）。

期望与方差的关系，二项分布的期望和方差是什么意思

推荐阅读

关于节约粮食的名言诗句关于节约粮食的名言和诗句

奋斗励志朋友圈句子励志短句致自己奋斗朋友圈

想发朋友圈表示心情不好的句子心情不好发朋友圈的句子心情短句

贝拉玻尿酸是合法的吗贝拉玻尿酸是进口的还是国产的

核桃仁做菜的菜谱，您知道桃仁脆溜鸡的做法

浅紫色显皮肤黑还是白

库伦旗景点

居家隔离和集中隔离的区别什么情况下要隔离28天

蝉蛹是什么

怎样能丰胸最安全有效