爱刨根知识网

  1. 首页 > 经验知识 > >

长方体几个面几个点几个棱

生活经验几个

长方体几个面几个点几个棱
【长方体几个面几个点几个棱】长方体有12条棱，8个顶点，6个面，长方体一共有12条棱，其中每4条相互平行的棱组成一组，长方体共三组4条相互平行的棱 。长方体相互平行的4条棱长度相等 。长方体相邻的两条棱相互垂直 。
长方体的长为a，宽为b，高为c，对角线长度为l，表面积为S，体积为V 。则长方体计算公式：
1、长方体的对角线长度
长方体对角线的平方=长的平方+宽的平方+高的平方，即l=√（a2+b2+c2） 。
2、长方体的表面积S
长方体的表面积等于长方体六个面的面积之和 。即S=ab+ab+bc+bc+ac+ac=2ab+2bc+2ac
3、长方形的体积V
长方形的体积=长x宽x高 。即V=a*b*c 。
长方形有几个面几个顶点几条棱相对面面积是什么相对论的长度是什么长方体有六个面，八个顶点，12条棱，相对面面积是相等的，相对棱的长度相等 。
长方体的特征：
1、长方体有6个面 。每组相对的面完全相同 。
2、长方体有12条棱，相对的四条棱长度相等 。按长度可分为三组，每一组有4条棱 。
3、长方体有8个顶点 。每个顶点连接三条棱 。三条棱分别叫做长方体的长，宽，高 。
4、长方体相邻的两条棱互相垂直 。

长方体几个面几个点几个棱

文章插图
扩展资料：
设一个长方体的长、宽、高分别为a、b、c，则它的表面积为S = (ab+bc+ca)×2，也等于2ab+2bc+2ca，还等于2（ab+bc+ca）；
公式：长方体的表面积=长×宽×2+宽×高×2+长×高×2，或：长方体的表面积=（长×宽+宽×高+长×高）×2 。
长方体的体积=长×宽×高 。
长方形的性质：
1、两条对角线相等；
2、两条对角线互相平分；
3、两组对边分别平行；
4、两组对边分别相等；
5、四个角都是直角 。
周长的公式：
1、圆：C=πd=2πr (d为直径，r为半径，π)
2、三角形的周长C = a+b+c(abc为三角形的三条边)
3、四边形：C=a+b+c+d（abcd为四边形的边长）
4、特别的：长方形：C=2(a+b) （a为长，b为宽）
5、正方形：C=4a（a为正方形的边长）
6、多边形：C=所有边长之和
7、扇形的周长：C = 2R+nπR÷180? (n=圆心角角度) = 2R+kR (k=弧度)
长方体有几个面长方体有6个面：面ABCD、面EFGH、面ABFE、面DCGH、面BCGF、面ADHE，12条棱：AB、BC、CD、AD、EF、FG、GH、HE、AE、BF、CG、DH，八个顶点：A、B、C、D、E、F、G、H.
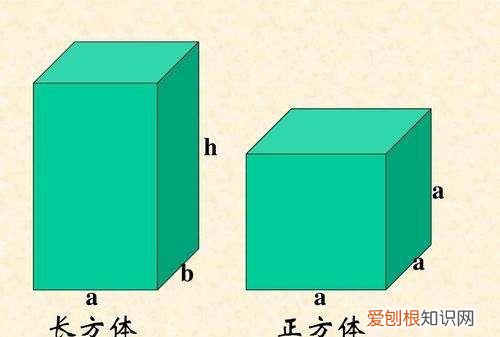
正方体和长方体都有几个面几个顶点几条棱正方体有6个面，12条棱，8个顶点 。长方体有6个面，12条棱，8个顶点 。
正方体每个顶点连接三条棱，每条棱长度相等，每个面面积相等 。长方体每组相对的面完全相同，相对的四条棱长度相等 。按长度可分为三组，每个顶点连接三条棱 。
长方体几个面几个点几个棱

文章插图
扩展资料一、正方体特征如下：
1、正方体有8个顶点，每个顶点连接三条棱 。
2、正方体有12条棱，每条棱长度相等 。
3、正方体有6个面，每个面面积相等 。
二、长方体特征如下：
1、长方体有6个面 。每组相对的面完全相同 。
2、 长方体有12条棱，相对的四条棱长度相等 。按长度可分为三组，每一组有4条棱 。
3、长方体有8个顶点 。每个顶点连接三条棱 。三条棱分别叫做长方体的长，宽，高 。
参考资料：
长方体由几个面几条棱几个顶点组成长方体由6个面，12条棱，8个顶点 。6个面都是长方形，有时两个相对面都是正方形，（相对）的面完全相同 。

推荐阅读


上一篇：蛹虫草拌鸡丝的做法，蛹虫草的功效与作用及食用方法

下一篇：生吃三文鱼怎么处理，生吃三文鱼前要清洗吗