爱刨根知识网

  1. 首页 > 经验知识 > >

如何判断异面直线，如何证明两条线是异面直线

生活经验如何

如何判断异面直线
异面直线证平行和垂直方法：根据“一条直线垂直于一个平面，则这条直线与这个平面上的所有直线都垂直” 。如果一条直线垂直于另一条直线所在的平面，则这两条异面直线垂直 。如果两条异面直线所成的角是直角，则称这两条异面直线互相垂直 。不同在任何一个平面内的两条直线叫做异面直线 。
定义法：由定义判定两直线永远不可能在同一平面内 。
定理：经过平面外一点和平面内一点的直线和平面内不经过该点的直线，是异面直线 。
记两条直线的方向向量分别为n1和n2，在两条直线上任取两个点，分别记为A和B 。如果向量AB、n1、n2三个向量的混合积(AB,n1,n2)不为零，那么这两条直线异面，否则共面 。
如何证明两条线是异面直线不同在任何一个平面内的两条直线叫做异面直线．异面直线的概念，在教学中既是重点又是难点，它的本质特征是既不相交又不平行的两条直线．
例
平面内一点与平面外一点的连线，和平面内不经过该点的直线是异面直线．(异面直线判定定理)
已知：直线a平面α，点Aα，点B∈平面α，Ba．
求证：直线AB与a是异面直线．
证明
假设直线AB与a共面β，则平面β∩α=a．
∵点B∈α∩β，∴点B∈a这与已知Ba矛盾．
∴假设是不正确的，∴AB与a是异面直线．
说明：以下证法是错误的，产生错误的原因是异面直线的概念不清．“∵aα，B∈α，Aα，∴AB和a不同在平面α内，∴AB与a异面．”对类似的错误，应该有所警惕．怎样证明两条直线异面呢？现在我们已知可以用三个方法，即利用异面直线的定义、利用异面直线的判定定理、利用反证法．
判断异面直线的方法有哪些在同一平面中，两条直线只有相交和平行的关系，没有第三种；从立体的角度就有异面直线了
异面直线是既不相交又不平行的直线，只要判断出着两条直线不在同一平面，而且不是平行的关系
【如何判断异面直线，如何证明两条线是异面直线】如一个长方体的一条棱的异面直线，只要找出既与它不在同一平面，又不和它相等的棱就行了（共2条）
怎样判断两条直线是否异面判定定理－平面内一点与平面外一点的连线,与此平面内不经过该点的直线是异面直线.
还可依据：
1.定义：不同在任何一个平面内的两条直线叫做异面直线
2.既不平行也不相交的两条直线是异面直线
异面直线的意思异面直线是不在同一平面上的两条直线 。异面直线是既不相交，又不平行的直线 。因为两条直线如果相交或平行，则它们必在同一平面上 。若无特别的说明，所说的空间直线，都是指异面直线 。
关于异面直线的错误说法：
1、分别在两个平面内的直线是异面直线；
2、在空间不相交的两条直线是异面直线；
3、平面内的一条直线和平面外的一条直线是异面直线 。

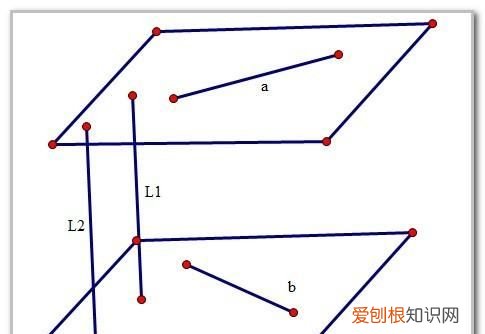
如何判断异面直线，如何证明两条线是异面直线

文章插图
扩展资料
判定方法——
(1)定义法：由定义判定两直线永远不可能在同一平面内，常用反证法 。
(2)判定定理：过平面外一点与平面内一点的直线和平面内不经过该点的直线是异面直线 。
例证：
判定定理：平面的一条交线与平面内不经过交点的直线互为异面直线 。
已知：AB∩α=A，CD?α，A?CD 。求证：AB和CD互为异面直线 。
证明：假设AB和CD在同一平面内，设这个平面是β 。即A∈β，CD?β 。
∵A∈α，CD?α，A?CD
以上就是关于如何判断异面直线，如何证明两条线是异面直线的全部内容，以及如何判断异面直线的相关内容,希望能够帮到您 。

推荐阅读


上一篇：正宗东坡肉的做法步骤 杭州名菜有哪些

下一篇：巡查员要几个王牌印记