二阶偏导数fxy怎么，二阶偏导数公式详解例题( 二 )

【二阶偏导数fxy怎么，二阶偏导数公式详解例题】?z/?y=-x·2y/2√(x2+y2)^(3/2)]=-xy/[(x2+y2)^(3/2)] 。
?2z/?x2=-(3/2)y2·2x/[(x2+y2)^(5/2)]=-3xy2/[(x2+y2)^(5/2)] 。
?2z/?x?y=[2y·[(x2+y2)^(3/2)-y2·(3/2)·[(x2+y2)^(1/2)2y]/[(x2+y2)3] 。

文章插图
1、当函数z=f(x,y)在(x0,y0)的两个偏导数f'x(x0,y0)与f'y(x0,y0)都存在时，我们称f(x,y)在(x0,y0)处可导。如果函数f(x,y)在域D的每一点均可导，那么称函数f(x,y)在域D可导。
2、求二阶偏导数的方法：当函数z=f(x,y)在(x0,y0)的两个偏导数f'x(x0,y0)与f'y(x0,y0)都存在时，我们称f(x,y)在(x0,y0)处可导。如果函数f(x,y)在域D的每一点均可导，那么称函数f(x,y)在域D可导。
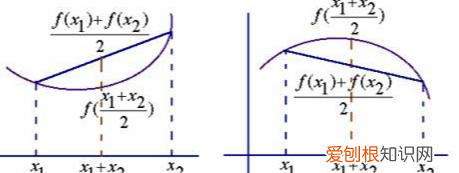
3、二阶导数的相关规定性质：设f(x)在[a,b]上连续，在（a,b)内具有一阶和二阶导数，那么，若在（a,b)内f''(x)>0,则f(x)在[a,b]上的图形是凹的；若在（a,b)内f''(x)<0,则f(x)在[a,b]上的图形是凸的。
4、结合一阶、二阶导数可以求函数的极值。当一阶导数等于0 ，而二阶导数大于0时，为极小值点。当一阶导数等于0 ，而二阶导数小于0时，为极大值点；当一阶导数和二阶导数都等于0时，为驻点。
以上就是关于二阶偏导数fxy怎么，二阶偏导数公式详解例题的全部内容，以及二阶偏导数fxy怎么求的相关内容,希望能够帮到您。

二阶偏导数fxy怎么，二阶偏导数公式详解例题( 二 )

推荐阅读

关于节约粮食的名言诗句关于节约粮食的名言和诗句

奋斗励志朋友圈句子励志短句致自己奋斗朋友圈

想发朋友圈表示心情不好的句子心情不好发朋友圈的句子心情短句

贝拉玻尿酸是合法的吗贝拉玻尿酸是进口的还是国产的

核桃仁做菜的菜谱，您知道桃仁脆溜鸡的做法

浅紫色显皮肤黑还是白

库伦旗景点

居家隔离和集中隔离的区别什么情况下要隔离28天

蝉蛹是什么

怎样能丰胸最安全有效