爱刨根知识网

  1. 首页 > 经验知识 > >

军棋游戏的玩法

生活经验军棋

本文主要讲解在 OpenHarmony 中军棋工兵寻径算法的实现 。

军棋游戏的玩法

文章插图
工兵可在铁路线上任意行走，其它棋子在铁路线上只能直走或经过弧形线，不能转直角弯；工兵在普通路线上跟其他棋子一样，走一格 。
但是在轨道上，就如入无人之地了 。可以在轨道上自由移动，怎样走都行，只要不超过轨道的区域，想走多远就走多远，但是如果有个棋子（不论敌我）堵住路 线，你就不能按照那个路线行进；同时我们还要寻找到最近的路径 。
军棋游戏的玩法

文章插图
算法分析
大体要求：
  • 工兵从起点到终点过程中不能有障碍物阻挡
  • 如何寻求到路径最短？且是否用时最快
  • 也有可能起点到终点是死路
军旗的工兵走法特别像迷宫走法 。
迷宫算法
深度优先搜索（DFS）：它和递归的探测思路是基本一致的，可以看成是递归方式的非递归版本；
广度优先搜索（BFS）：广度优先搜索法利用队列的特点，一层层向外扩展查找可走的方块，直到找到出口为止，最先找到的这个答案就必然是最短的 。
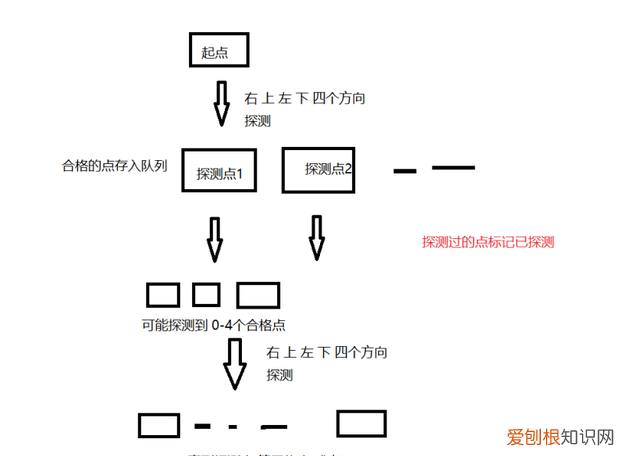
根据特点我们希望最先找到最短的距离故采用 bfs 的方式；采用队列来记录探测点；当前探测点的四个方向，可以通过的点，保存到这个队列中，并移除当前探测点 。
军棋游戏的玩法

文章插图
右下左上的四个方向探测：
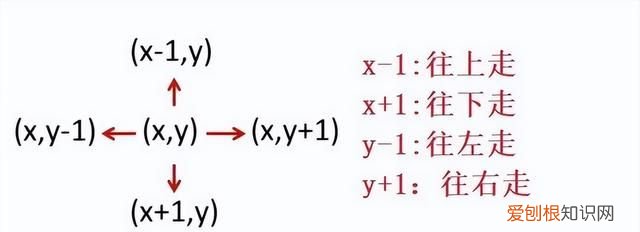
军棋游戏的玩法

文章插图
采用一个二维数组来存储 x，y 上的障碍物，和探测的点：
let noChessBoard: number[][] = [ // a[j][h]代表j行h列数据 // 1,行：row 2、列：column export const ROW = 12 export const COLUMN = 4 [1, 1, 1, 1, 1], [0, 0, 0, 0, 0], [0, 1, 1, 1, 0], [0, 1, 1, 1, 0], [0, 1, 1, 1, 0], [0, 0, 0, 0, 0], [0, 1, 0, 1, 0], [0, 0, 0, 0, 0], [0, 1, 1, 1, 0], [0, 1, 1, 1, 0], [0, 1, 1, 1, 0], [0, 0, 0, 0, 0], [1, 1, 1, 1, 1]]代码实现
①获取到起点和终点坐标
this.routeNode = this.engineerRoute(firstChess, moveChess);【军棋游戏的玩法】②获取二维数组迷宫标记
二维数组是记录棋盘上 0 是表示可通状态，1 表示不可通 。默认是棋盘铁路都为 0 可通 。
然后，敌方和友方其中全部设置为不可通 1：
// 工兵路径寻找 （bfs 广度优先搜索）private engineerRoute(start: Chess, end: Chess): RouteNode { let noChessBoard: number[][] = [ // a[j][h]代表j行h列数据 // 1,行：row 2、列：column export const ROW = 12 export const COLUMN = 4 [1, 1, 1, 1, 1], [0, 0, 0, 0, 0], [0, 1, 1, 1, 0], [0, 1, 1, 1, 0], [0, 1, 1, 1, 0], [0, 0, 0, 0, 0], [0, 1, 0, 1, 0], [0, 0, 0, 0, 0], [0, 1, 1, 1, 0], [0, 1, 1, 1, 0], [0, 1, 1, 1, 0], [0, 0, 0, 0, 0], [1, 1, 1, 1, 1]] for (let i = 0;i < this.aList.length; i++) { let a = this.aList[i] noChessBoard[a.y][a.x] = 1 } for (let i = 0;i < this.bList.length; i++) { let b = this.bList[i] noChessBoard[b.y][b.x] = 1 } return this.bfs(start, end, noChessBoard)}③进行广度优先搜索
private bfs(start: Chess, end: Chess, roads: number[][]): RouteNode{ Logger.d(TAG, `bfs roads:${JSON.stringify(roads)}`) Logger.d(TAG, `bfs start:${JSON.stringify(start)}`) Logger.d(TAG, `bfs end:${JSON.stringify(end)}`) let routeQueue = new MyArrayQueue() let first = new RouteNode(start.x, start.y, 0) routeQueue.push(first) while (routeQueue.size() != 0) { Logger.d(TAG, `bfs scan while routeQueue:${JSON.stringify(routeQueue)}`) let node = routeQueue.pop() Logger.d(TAG, `bfs scan pop node:${JSON.stringify(node)}`) let x = node.x let y = node.y if (x === end.x && y === end.y) { return node // break } for (var i = 0; i < 4; i++) { let tx = x + this.dx[i] let ty = y + this.dy[i] Logger.d(TAG, `bfs scan tx:${tx} ty:${ty}`) if (tx >= 0 && tx <= COLUMN && ty >= 0 && ty <= ROW && roads[ty][tx] === 0) { // 如果该位置可以走动 // 入队 Logger.d(TAG, `bfs add tx:${tx} ty:${ty}`) let temp = new RouteNode(tx, ty, node.step + 1) temp.prev = node routeQueue.push(temp) Logger.d(TAG, `bfs scan push :${JSON.stringify(routeQueue)}`) roads[ty][tx] = 1 } } // 扩展完 Logger.d(TAG, `bfs scan one end...`) } return null}

推荐阅读


上一篇：原味苦瓜干片,给老妈晒苦瓜片

下一篇：文件怎么加密?哪款文件加密软件最好用呢