具有鲜明的直观性,以表象,标准差可以做哪些图表

选自 Fahd Alhazmi's Blog
机器之心编译
参与：魔王、杜伟

本文将对标准差这一概念提供直观的视觉解释。

文章插图
本文作者为纽约市立大学在读博士生 Fahd Alhazmi，专注于神经科学、人工智能和人类行为研究。
统计学中最核心的概念之一是：标准差及其与其他统计量（如方差和均值）之间的关系。入门课程中老师常告诉学生「记住公式就行」，但这并非解释概念的最佳方式。本文将对标准差这一概念提供直观的视觉解释。
假设你有一个成绩单，在本案例中这即是现实测量（real-world measurements）。我们想将这些测量中的信息「压缩」为一组量，以便后续对比不同班级的成绩或不同年份的成绩等。鉴于认知能力有限，我们不想挨个查看分数，来找出平均分更高的班级。这时就需要总结数字，描述统计学就派上用场了。
总结数字的方式有两种：量化其相似性或差异（difference）。

量化数字的相似性即「集中趋势量数」（measures of central tendency），包括平均数、中位数和众数；
量化数字的差异即「差异量数」（measures of variability），包括方差和标准差。

标准差揭示一组数字中彼此之间的差异，以及数字与平均值之间的差异。
举例而言，假设你收集了一些学生分数（出于简洁性考虑，我们假设这些分数是总体）。

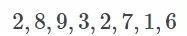
文章插图
我们首先在简单的散点图中绘制这些数字：

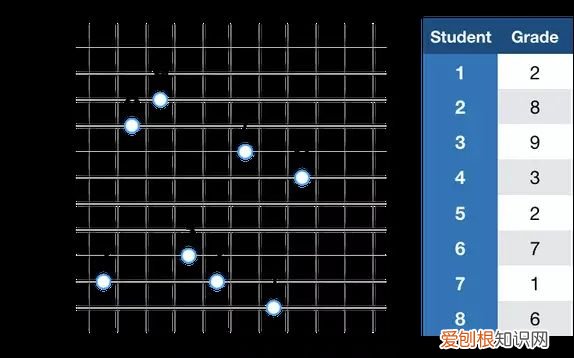
文章插图
绘制完成后，计算差异的第一步是找出这些数字的中心，即平均值。

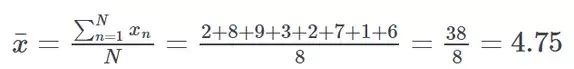
文章插图
视觉上，我们可以绘制一条线来表示平均分数。

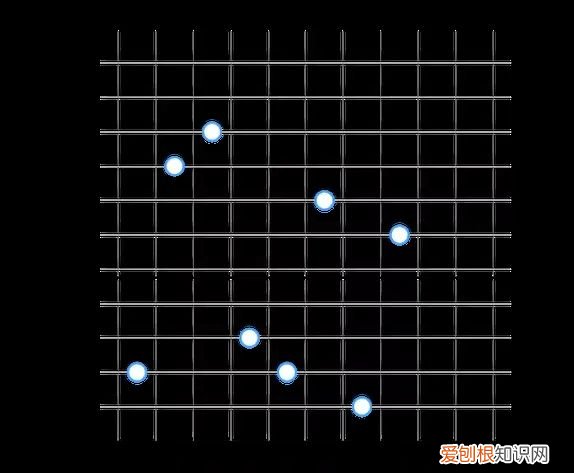
文章插图
接下来我们要计算每个点和平均值之间的距离，并对得到的数值求平方。记住，我们的目标是计算数字之间的差异，以及数字与平均值之间的差异。我们可以用数学或视图的方式完成该操作：

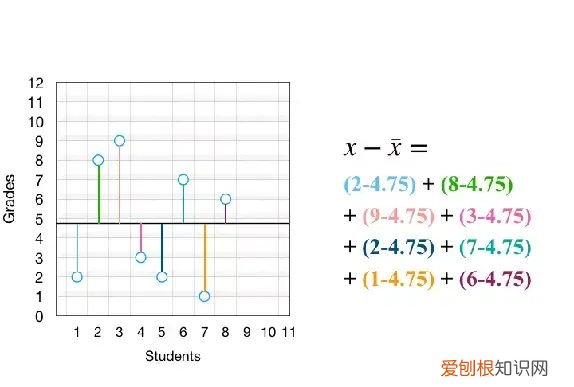
文章插图
从上图中我们可以看到，「求平方」只不过是画了一个方框而已。这里有两点需要注意：我们无法计算所有差异的总和。因为一些差异是正值，一些是负值，求和会使正负抵消得到 0 。为此，我们对差异取平方（稍后我会解释为什么取平方而不是其他运算，如取绝对值）。
现在，我们来计算差异平方的总和（即平方和）：

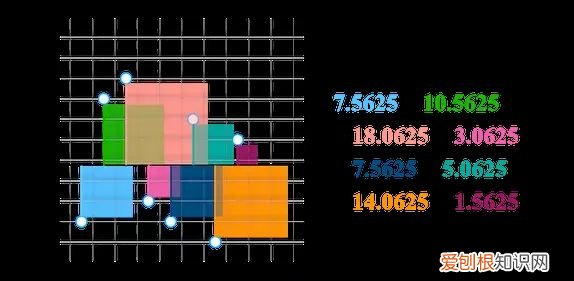
文章插图
通过计算平方和，我们高效计算出这些分数的总变异（即差异）。理解变异（variability）与差异（difference）之间的关系是理解多个统计估计和推断检验的关键。上图中平方和 67.5 表示，如果我们将所有方框堆在一个巨大的正方形中，则大正方形的面积等于 67.5 points^2，points 指分数的单位。任意测量集的总变异都是正方形的面积。
方差
现在我们得到了总变异（即大正方形的面积），但我们真正想要的是平均变异（mean variability）。要想求得平均变异，我们只需要用总面积除以方框的数量：

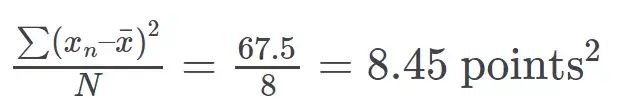
文章插图

文章插图
出于实用目的考虑，你或许想除以 N?1，而不是 N，这样你就可以尝试基于一个样本而不是总体来估计平均变异。但是，这里假设我们已经具备总体（total population）。重点在于，你想计算所有小方框的均方值。这就是「方差」，即平均变异，或者差异平方的平均值（mean squared difference）。

具有鲜明的直观性,以表象,标准差可以做哪些图表

推荐阅读

关于节约粮食的名言诗句关于节约粮食的名言和诗句

奋斗励志朋友圈句子励志短句致自己奋斗朋友圈

想发朋友圈表示心情不好的句子心情不好发朋友圈的句子心情短句

贝拉玻尿酸是合法的吗贝拉玻尿酸是进口的还是国产的

核桃仁做菜的菜谱，您知道桃仁脆溜鸡的做法

浅紫色显皮肤黑还是白

库伦旗景点

居家隔离和集中隔离的区别什么情况下要隔离28天

蝉蛹是什么

怎样能丰胸最安全有效