爱刨根知识网

  1. 首页 > 经验知识 > >

一元n次方程有几个根

生活经验一元

一元n次方程有几个根
一元n次方程有n个根，包括实根虚根 。一元n次方程，存在无实数解的情况 。如果有实数，那么n次方程就有n个实数根 。这n个实数根，可能互不相等，也可能相等 。
例如：
【一元n次方程有几个根】一元二次方程，如果判别式小于0，那就没有实数根 。如果判别式等于0，那就有2个相等的实数根；如果判别式大于0，那就有2个不相等的实数根 。
一元n次方程有几个根一元多次方程整数解的个数用求根公式进行解决 。
一元一次方程、一元二次方程、一元三次方程分别有一个根、二个根、三个根，它们都可以用代数解法来解，并且有求根公式 。
可以证明一元四次方程有四个根，并且可以用代数解法求解 。当n > 4时，根据伽罗华理论，一般形式的n次方程不能用代数解法来解 。

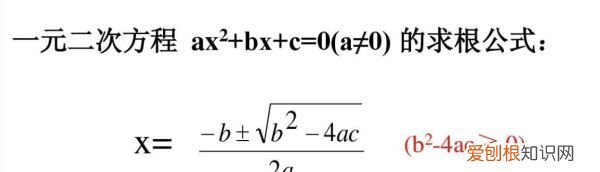
一元n次方程有几个根

文章插图
一元n次方程的根的个数定理和推论：
一元n次方程至少有一个根，如果f (x )的次数大于1, 那么根据定理1可以知道，方程f (x) =0至少有一个根 。
设这个根是α，那么由于f(α) =0，根据因式定理可以知道，f(x)=(x-α)q(x)，因为x-α和q (x)的次数都低于f(x)的次数，所以f(x)可约 。
例如，方程(x-2)3(x+1)2(x-1)=0有三重根2，二重根-1，単根1，因此，这个方程一共有6个根 。
一元n次方程的n个根之和是什么?一元n次方程的n个根之和是-a (n-1) 。
假设一元n次方程a0xn+a1xn-1+…＋an=0（a0≠0）的n个解为y(i),其中i是从1到n的整数 。则有等式为（x-y（1））（x-y（2））…（x-y（n））＝0，分解等式得x^（n-1）项的系数为－∑y（i）＝a（n-1），则∑b（i）＝-a（n-1） 。
一元n次方程有几个根

文章插图
性质：
1、一元n次方程至少有一个根 。一元n次方程有n个根并且只有n个根 。
2、任何次数大于1的多项式都是可约的 。
3、一元一次方程、一元二次方程、一元三次方程分别有一个根、二个根、三个根，它们都可以用代数解法来解，并且有求根公式 。
为什么一元几次方程就有几个根请说说原理因为n次方程可表为
（x-x1)(x-x2)……(x-xn)=0
故有n个根
一元n次方程在不考虑重跟及复数根的前提下有n个根第一问有点看不明白，若重根和复数根都计数的话，一元n次方程必然有n个根，这是代数基本定理 。
一元三次方程除非是某些特殊的形式，否则没有什么因式分解的技巧 。或者可以观察出某一个解x=k，然后利用多项式除法，用原方程除以x-k得到剩余的二次多项式，最后对二次多项式进行因式分解 。
当然还可以用通用的一元三次方程的公式解法（可百度“卡尔丹公式”或“卡尔丹方法”）求出方程的三个根，自然就得到了因式分解的结果 。例如原方程ax3+bx2+cx+d=0的根为x1,2,3，那么其因式分解形式为：
a(x-x1)(x-x2)(x-x3)=0
以上就是关于一元n次方程有几个根的全部内容，以及一元n次方程有几个根的相关内容,希望能够帮到您 。

    推荐阅读


    上一篇：被称为万园之园的皇家园林是

    下一篇：原神勾勾果多久刷新一次