连续函数的原函数连续吗
原函数连续 。因为F(x)的导数等于f(x),F(x)叫做f(x)的一个原函数,这里就已经表明了F(x)是可求导的,一元函数可导一定连续的,所以原函数F(x)一定连续 。
连续函数在直角坐标系中的图像是一条没有断裂的连续曲线 。由极限的性质可知,一个函数在某点连续的充要条件是它在该点左右都连续 。
连续函数的原函数总是存在连续函数的原函数存在,因为分段函数也有原函数,比如像X=Y(X≠1)的原函数就是X=Y(X≠1),连续函数必然可积,函数可积不一定连续,也就是说,不连续的函数也有可能可积 。
函数在数学上的定义:给定一个非空的数集A,对A施加对应法则f,记作f(A),得到另一数集B,也就是B=f(A) 。那么这个关系式就叫函数关系式,简称函数 。
连续函数的原函数一定连续吗一定连续!请你回想下原函数的定义,F(x)的导数等于f(x),F(x)叫做f(x)的一个原函数 。这里就已经表明了F(x)是可求导的,一元函数可导一定连续的,所以原函数F(x)一定连续 。其实这里面呢是f(x)未必连续的 。
fx有原函数,原函数一定连续吗是 。因为连续函数一定有原函数,积分上限函数是该导函数的一个原函数,切积分上限函数一定连续,所以导函数连续原函数一定连续 。
f(x)的一阶导数连续,f(x)当然可导(假设了导数不但存在且连续);f(x)的原函数一定可导:因为f(x)可导,当然f(x)连续,其原函数当然可导:其原函数即f(x) 。
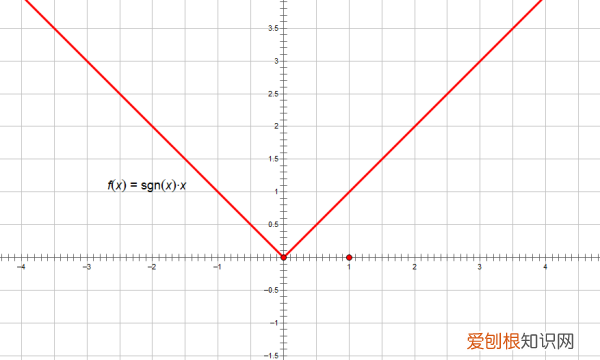
文章插图
函数可导的条件:
如果一个函数的定义域为全体实数,即函数在其上都有定义 。函数在定义域中一点可导需要一定的条件:函数在该点的左右导数存在且相等,不能证明这点导数存在 。只有左右导数存在且相等,并且在该点连续,才能证明该点可导 。
【连续函数的原函数连续,连续函数的原函数总是存在】可导的函数一定连续;连续的函数不一定可导,不连续的函数一定不可导 。
连续函数必有原函数这句话对吗对的 。
可导必连续 。导函数连续,则原函数可导,所以原函数连续 。
连续函数列的极限函数连续不是 。连续必有极限,有极限未必连续 。一个函数f(x)在点x0处连续必须有三个条件:
1、函数f(x)在点x0处有定义;
2、函数f(x)在点x0处有极限;
3、函数f(x)在点x0处的极限等于该点的函数值f(x0) 。
这三个条件缺一不可,是判断函数在该点连续的充要条件,因此说函数有极限是函数连续的必要不充分条件 。至于函数在区间上的连续,开区间两个端点处是否连续并不要求;闭区间的在左端点要求右连续,右端点要求左连续 。

文章插图
以上就是关于连续函数的原函数连续,连续函数的原函数总是存在的全部内容,以及连续函数的原函数连续吗的相关内容,希望能够帮到您 。
推荐阅读
- 用什么水给宝宝冲奶粉最好
- 陌陌发朋友圈的句子 陌陌朋友圈说说
- 一个月婴儿一天尿几次
- 献血浆为什么会给钱,为什么献全血没有钱而献血浆却有钱呢
- 发朋友圈情感经典句子 发朋友圈的十句情感语录说说
- 40天宝宝拉肚子能不能吃米油
- 超市地下停车场晚上能停车,永辉超市地下停车场收费吗
- 不锈钢水壶如何挑选 什么型号不锈钢水壶比较好
- 新生儿一天拉几次尿


