lnx是有界函数吗【lnx是有界函数,lnx为什么不是有界函数】
lnx不是有界函数 , lnx是一种常见的对数函数 。有界函数并不一定是连续的 , 根据定义 , ?在D上有上(下)界 , 则意味着值域?(D)是一个有上(下)界的数集 。
有界函数是设f(x)是区间E上的函数 , 若对于任意的x属于E , 存在常数m、M , 使得m≤f(x)≤M , 则称f(x)是区间E上的有界函数 。其中m称为f(x)在区间E上的下界 , M称为f(x)在区间E上的上界 。
lnx为什么不是有界函数lnx在(1,2)上有界 ,
当然lnx在(1,3)上也是有界 ,
具体说在哪个区间 , 当然和具体的题目有关 。
lnx为什么不是有界函数首先lnx在其一般定义域(0 , +∞)上是无界的 , 而lnx在(0 , +∞)上并不可积 。
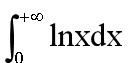
文章插图
lnx在其一般定义域上的积分
需要注意的是 , 可积指的是在某个区间(若无特殊强调则为定义域)上的定积分结果存在 , 需要和该函数存在原函数(也就是不定积分存在)这一点区分开来 。
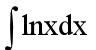
文章插图
lnx的不定积分
x→0、x→+∞时 , lnx→-∞、+∞ , 所以对于lnx在定义域上的积分 , 处理步骤如下:
① 解出不定积分∫lnxdx=xlnx-x+C
② 求出不定积分在0、+∞处的极限值 , 对于此题 , 0处极限为-∞ , +∞处极限为+∞
③ 所以该不定积分的结果可以看成+∞ , +∞无法作为积分结果 , 所以可以说该积分发散
④ 得出结论:lnx在其定义域上并不可积 。
函数y=lnx在区间(0,1)内是否有界连续函数在闭区间上必有界 , 该函数为基本初等函数 , 也为连续函数 , 所以只要给定的区间是闭区间 , 必有界 。记住一定是闭区间 。
lnx是有界函数吗lnx是无界函数 , x趋于正无穷时 , lnx趋于正无穷 。

文章插图
linx是有界函数lnx不是有界函数 , lnx是一种常见的对数函数 。有界函数并不一定是连续的 , 根据定义 , ?在D上有上(下)界 , 则意味着值域?(D)是一个有上(下)界的数集 。
有界函数是设f(x)是区间E上的函数 , 若对于任意的x属于E , 存在常数m、M , 使得m≤f(x)≤M , 则称f(x)是区间E上的有界函数 。其中m称为f(x)在区间E上的下界 , M称为f(x)在区间E上的上界 。
以上就是关于lnx是有界函数 , lnx为什么不是有界函数的全部内容 , 以及lnx是有界函数吗的相关内容,希望能够帮到您 。
推荐阅读
- 朱棣当了皇帝后怎么对待朱允炆的
- 试纸最早几天能测出来,怀孕试纸多少天能试出来
- 陶片放逐法的特点
- 养金鱼多久加一次盐
- 电脑登录QQ忘记退出了怎么办
- 凸轮连杆机构简图 凸轮设计的步骤
- 对于等离子体技术的分析 等离子体技术的发展及应用前景
- 陈皮三宝茶有什么功效
- 改善脾胃的10步法 如何调理脾胃的方法


