单位正交列向量是什么意思，为什么正交矩阵的行向量是单位向量

单位正交列向量是什么意思
单位正交列向量指的是x、y内积为0，即x的转置乘y为0，而其分量平方和为1，指的是单位正交向量。在三维向量空间中，两个向量的内积如果是零，那么就说这两个向量是正交的。
“正交向量”是一个数学术语，指点积为零的两个或多个向量。几何向量的概念在线性代数中经由抽象化，得到更一般的向量概念。此处向量定义为向量空间的元素，要注意这些抽象意义上的向量不一定以数对表示，大小和方向的概念亦不一定适用。正交最早出现于三维空间中的向量分析。换句话说，两个向量正交意味着它们是相互垂直的。若向量α与β正交，则记为α⊥β 。
为什么正交矩阵的行向量是单位向量因为正交不需要单位，但是可能是数学界的习惯，定义称必须是单位向量了。
A是正交矩阵。
<=> A^TA=E (定义) 。
<=> A的行(列)向量两两正交且是单位向量 (定理) 。
将A按列分块为 A=(a1，an) 。
由 A^TA=E得 ai^Taj = 1 (i=j) , 0 (i≠j) 。
【单位正交列向量是什么意思，为什么正交矩阵的行向量是单位向量】所以列向量ai是单位向量, 且两两正交。
同理由 AA^T=E可得A的行向量也是两两正交的单位向量。
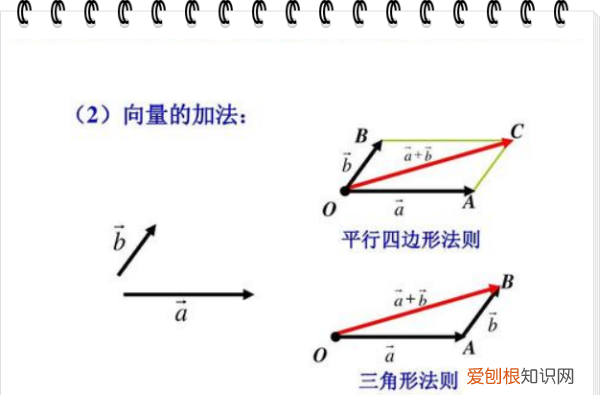
向量的记法：
印刷体记作粗体的字母（如a、b、u、v），书写时在字母顶上加一小箭头“→” 。如果给定向量的起点（A）和终点（B），可将向量记作AB（并于顶上加→）。在空间直角坐标系中，也能把向量以数对形式表示，例如Oxy平面中(2,3)是一向量。
向量组与向量正交是什么意思向量正交指点积为零的两个或多个向量。向量组的基本判定是：两个向量组可以互相线性表示。
1、向量正交
在三维向量空间中，如果两个向量的内积为零，则两个向量是正交的。正交性最早出现在三维空间的矢量分析中。换句话说，两个向量的正交性意味着它们彼此垂直。在物理学和工程学中，几何矢量通常称为矢量。
许多物理量都是矢量，例如物体的位移、球对墙的作用力等等。相反，它是一个标量，即一个只有大小但没有方向的量。一些与矢量有关的定义也与物理概念密切相关，如物理学中与势能相对应的矢量势。
2、向量组
（1）等价向量具有传递性、对称性和自反性。但是向量的数目可以不同，线性相关性也可以不同。
（2）任何向量组都等价于其最大独立群。
（3）向量组的任意两个最大独立群是等价的。
（4）两个等价的线性独立向量组中包含的向量数目相同。
（5）等价向量组具有相同的秩，但具有相同秩的向量组不一定等价。
（6）如果向量组a可以由向量组b线性表示，且R（A）=R（B），则A与B等价。

文章插图
扩展资料：
向量组A：a1，a2，…am与向量组B：b1，b2，…bn的等价秩相等条件是R（A）=R（B）=R（A，B），其中A和B是向量组A和B所构成的矩阵。（注意区分粗体字与普通字母所表示的不同意义。）
对两个向量x和y有内积性质(x,ky)=k(x,y) 。两个向量组可以互相线性表示，则称这两个向量组等价。在空间直角坐标系中，也能把向量以数对形式表示，例如Oxy平面中用(2,3)表示向量。向量正交（勾股定理）如果α⊥β，则有

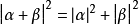
文章插图
a,b正交且为单位向量什么意思两个向量均正交的向量就是求法向量，可以先设出法向量，再利用与两个已知向量都等于零，解方程组即可，法向量不唯一，但是它们是共线的与两个向量正交的向量?与两个向量都正交的单位向量,一般是指与坐标轴正方向相同的单位向量,如果要加正负号,也能构成单位向量

单位正交列向量是什么意思，为什么正交矩阵的行向量是单位向量

推荐阅读

关于节约粮食的名言诗句关于节约粮食的名言和诗句

奋斗励志朋友圈句子励志短句致自己奋斗朋友圈

想发朋友圈表示心情不好的句子心情不好发朋友圈的句子心情短句

贝拉玻尿酸是合法的吗贝拉玻尿酸是进口的还是国产的

核桃仁做菜的菜谱，您知道桃仁脆溜鸡的做法

浅紫色显皮肤黑还是白

库伦旗景点

居家隔离和集中隔离的区别什么情况下要隔离28天

蝉蛹是什么

怎样能丰胸最安全有效