无穷小怎么判断高低阶
当x趋向于0时,极限值为0 。f(x)为g(x)的高阶无穷小 。当x趋向于0时,极限值为无穷 。f(x)为g(x)的低阶无穷小 。当x趋向于0时,极限值为一个常数 。f(x)为g(x)的同阶无穷小 。当x趋向于0时,极限值为1 。f(x)为g(x)的等阶无穷小 。
无穷小是数学分析中的一个概念,用以严格定义诸如“最终会消失的量”、“绝对值比任何正数都要小的量”等非正式描述,即以数0为极限的变量,无限接近于0 。根据常数所对应的阶数就可以看出是几阶无穷小 。设这个函数是f(x),则计算极限lim(x->0)f(x)/x^n,如果当n=p-1时,极限值=0 。当n=p时,极限值=常数,则可以判断,f(x)是x^p的同阶无穷小,当这个常数=1时,f(x)是x^p的等价无穷小 。
如何判断等阶无穷小判断如下:
设这个函数是f(x),则计算极限lim(x->0) f(x)/x^n,如果当n=p-1时,极限值=0 。当n=p时,极限值=常数,则可以判断,f(x)是x^p的同阶无穷小,当这个常数=1时,f(x)是x^p的等价无穷小 。
无穷小是数学分析中的一个概念,用以严格定义诸如“最终会消失的量”、“绝对值比任何正数都要小的量”等非正式描述,即以数0为极限的变量,无限接近于0 。根据常数所对应的阶数就可以看出是几阶无穷小 。

文章插图
简介:
无穷小量是数学分析中的一个概念,在经典的微积分或数学分析中,无穷小量通常以函数、序列等形式出现 。
无穷小量即以数0为极限的变量,无限接近于0 。确切地说,当自变量x无限接近x0(或x的绝对值无限增大)时,函数值f(x)与0无限接近,即f(x)→0(或f(x)=0),则称f(x)为当x→x0(或x→∞)时的无穷小量 。特别要指出的是,切不可把很小的数与无穷小量混为一谈 。
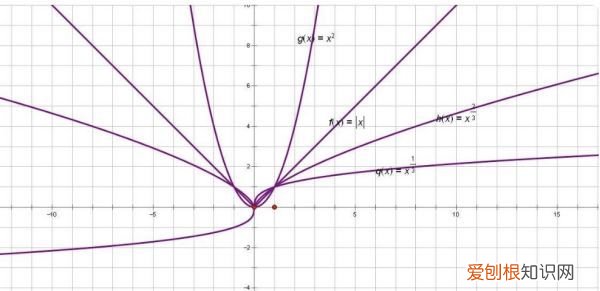
高阶无穷小要看函数的次方来判断 。
例如:x平方和x三次方中,x平方就是低阶,x三次方就是高阶 。
如果存在M>0,对于一切属于区间X上的x,恒有|f(x)|≤M,则称f(x)在区间X上有界,否则称f(x)在区间上无界 。
如果对于区间上任意两点x1及x2,当x1
文章插图
扩展资料:
当平面直角坐标系中两直线平行时,其函数解析式中k的值(即一次项系数)相等;当平面直角坐标系中两直线垂直时,其函数解析式中k的值互为负倒数(即两个k值的乘积为-1) 。
从函数的角度看,解不等式的方法就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围的一个过程 。
从函数图像的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合 。
如何判断等阶无穷小利用定义或者求导判断 。
如:x→0时,x3+x2/x2=1,故x3+x2为二阶 。
结论:无穷小的阶数由其中的最低阶决定 。
求N阶导之后变成不是无穷小它就是N阶无穷小 。
无穷小量是数学分析中的一个概念,在经典的微积分或数学分析中,无穷小量通常以函数、序列等形式出现 。
无穷小量即以数0为极限的变量,无限接近于0 。确切地说,当自变量x无限接近x0(或x的绝对值无限增大)时,函数值f(x)与0无限接近,即f(x)→0(或f(x)=0),则称f(x)为当x→x0(或x→∞)时的无穷小量 。特别要指出的是,切不可把很小的数与无穷小量混为一谈 。
推荐阅读
- 硬笔如何运笔,硬笔书法运笔发力的技巧
- 怎么创建个人微信订阅号,如何创建个人微信公众号?
- 杭州哪个区外卖单子多
- 院中不知种啥好 庭院围墙种爬藤植物风水好吗
- 借钱不还起诉书范文 民事诉讼状
- 刘备称帝合法吗 排盘八字元亨利贞
- 在风水学上松树和柏树是一样的吗 桑树风水化解
- 杨子前妻陶虹现在结婚了吗 陶虹的老公
- 寓意发财的植物小盆栽 什么花寓意发财好运


