方向余弦怎么，已知方向向量求直线方程

方向余弦怎么求
方向余弦，指的是三维空间中，向量与三条坐标轴的夹角余弦值。本文，就来介绍一下方向余弦的计算方法。
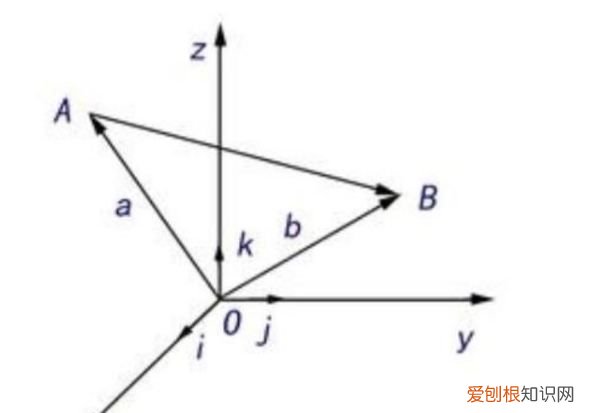
三维空间中，点A代表向量OA ，其中O是原点。
设OA={a,b,c} ，它与x轴的夹角，可以通过向量点乘来计算。
x轴可以用向量{1,0,0}代替：
A.{1,0,0}/Sqrt[A.A]
y轴可以用向量{0,1,0}代替：
A.{0,1,0}/Sqrt[A.A]
z轴可以用{0,0,1}代替：
A.{0,0,1}/Sqrt[A.A]
因此，向量OA的方向余弦，也是一个三维向量：
vec=A.#/Sqrt[A.A]/@IdentityMatrix[3]
方向余弦的长度等于1：
vec.vec//Factor
已知方向向量求直线方程方向(x ， y ， z) 的方向余弦 (x ， y ， z)/√(x^2+y^2+z^2) ，也就是把它单位化就是了，所以 {1,4,-8) 的方向余弦是 (1 ， 4 ， -8)/9 。
已知定点P0（x0 ， y0 ， z0)及非零向量v={l ， m ， n} ，则经过点Pο且与v平行的直线L就被确定下来，因此，点P0与v是确定直线L的两个要素。
由于对向量的模长没有要求，所以每条直线的方向向量都有无数个。直线上任一向量都平行于该直线的方向向量。

文章插图
扩展资料：
【方向余弦怎么，已知方向向量求直线方程】因为方向不能比较大小，所以向量也就不能比较大小。对于向量来说“大于”和“小于”的概念是没有意义的。
如果向量AB与向量CD的模相等且方向相反，那么我们把向量AB叫做向量CD的负向量。当用有向线段表示向量时，起点可以任意选取。任意两个相等的非零向量，都可用同一条有向线段来表示，并且与有向线段的起点无关．同向且等长的有向线段都表示同一向量。
向量的方向余弦怎么算设向量a={x,y,z}, 向量a°是向量a的单位向量, |a°|=1；
则 a°=(cosα)i+(cosβ)j+(cosγ)k, 式中,i,j,k 是坐标单位向量；
式中,α,β,γ就叫做向量的方向角；cosα,cosβ,cosγ就叫做方向余弦。
介绍：

文章插图
方向余弦是指在解析几何里，一个向量的三个方向余弦分别是这向量与三个坐标轴之间的角度的余弦。两个向量之间的方向余弦指的是这两个向量之间的角度的余弦。
“方向余弦矩阵”是由两组不同的标准正交基的基底向量之间的方向余弦所形成的矩阵。方向余弦矩阵可以用来表达一组标准正交基与另一组标准正交基之间的关系，也可以用来表达一个向量对于另一组标准正交基的方向余弦。
运用：
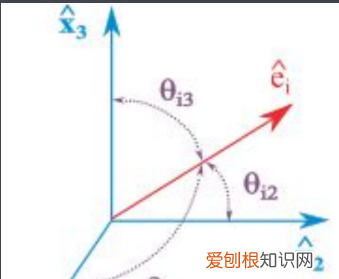
设有空间两点，若以P1为始点，另一点P2为终点的线段称为有向线段。通过原点作一与其平行且同向的有向线段，将与Ox,Oy,Oz三个坐标轴正向夹角分别记作α,β,γ 。
这三个角α,β,γ称为有向线段的方向角，其中0≤α≤π,0≤β≤π,0≤γ≤π 。若有向线段的方向确定了，则其方向角也是唯一确定的。
方向角的余弦称为有向线段或相应的有向线段的方向余弦。
三元函数的方向余弦怎么求方向余弦计算公式为：cosa=ax/|a| 。方向余弦是指在解析几何里，一个向量的三个方向余弦分别是这向量与三个坐标轴之间的角度的余弦。两个向量之间的方向余弦指的是这两个向量之间的角度的余弦。几何就是研究空间结构及性质的一门学科。
两点间的方向余弦怎么求设：A（x1,y1,z1）,B（x2,y2,z2）.
向量AB的方向余弦＝｛（x2-x1）/d,（y2-y1）/d.（z2-z1）/d｝
其中， d＝|AB|＝√[（x2-x1）2+（y2-y1）2+（z2-z1）2]
（x2-x1）/d＝cosα.,（y2-y1）/d＝cosβ..（z2-z1）/d＝cosγ
其中：α,β,γ是向量AB分别与x轴。y轴， z轴所成的夹角[0≤α,β,γ≤π]
故称方向余弦。
以上就是关于方向余弦怎么，已知方向向量求直线方程的全部内容，以及方向余弦怎么求的相关内容,希望能够帮到您。

方向余弦怎么，已知方向向量求直线方程

推荐阅读

关于节约粮食的名言诗句关于节约粮食的名言和诗句

奋斗励志朋友圈句子励志短句致自己奋斗朋友圈

想发朋友圈表示心情不好的句子心情不好发朋友圈的句子心情短句

贝拉玻尿酸是合法的吗贝拉玻尿酸是进口的还是国产的

核桃仁做菜的菜谱，您知道桃仁脆溜鸡的做法

浅紫色显皮肤黑还是白

库伦旗景点

居家隔离和集中隔离的区别什么情况下要隔离28天

蝉蛹是什么

怎样能丰胸最安全有效