爱刨根知识网

  1. 首页 > 经验知识 > >

二叉树上元素之间呈现什么关系

生活经验二叉

二叉树上元素之间呈现什么关系
二叉树上的元素之间呈现一对多关系，二叉树（Binarytree）是树形结构的一个重要类型，许多实际问题抽象出来的数据结构往往是二叉树形式 。
二叉树特点是每个结点最多只能有两棵子树，且有左右之分 。二叉树是n个有限元素的集合，该集合或者为空、或者由一个称为根（root）的元素及两个不相交的、被分别称为左子树和右子树的二叉树组成，是有序树 。当集合为空时，称该二叉树为空二叉树 。
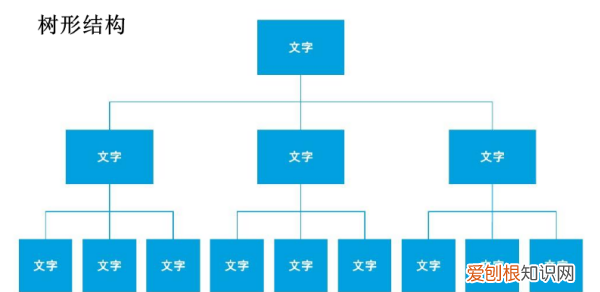
树形结构中元素之间存在什么关系呢一对多关系 。
树形结构中元素之间存在一对多的关系 。数据结构中，使用树形结构表示数据表素之间一对多的关系，树形结构是一种非线型结构 。
树(Tree)是n(n≥0)个相同数据类型的数据元素的集合，树中的数据元素称为节点(Node) 。n=0的树称为空树(Empty Tree)；对于n＞0的任意非空树T有：
1、有且仅有一个特殊的结点称为树的根(Root)结点，根没有前驱结点；
2、若n＞1，则除根结点外，其余结点被分成了m(m＞0)个互不相交的集合T1，T2，…，Tm，其中每一个集合Ti(1≤i≤m)本身又是一棵树 。树T1，T2，…，Tm称为这棵树的子树(Subtree) 。
总结：由树的定义可知，树的定义是递归的，用树来定义树 。因此，树（以及二叉树）的许多算法都使用了递归 。这里的一对多是是指行的对应 。

二叉树上元素之间呈现什么关系

文章插图
扩展资料
相关术语
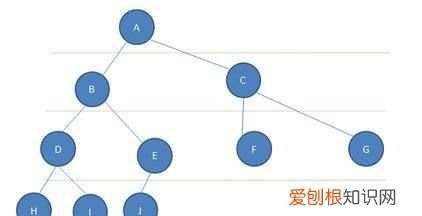
1、结点(Node)：表示树中的数据元素，由数据项和数据元素之间的关系组成 。在图中，共有10个结点 。
2、结点的度(Degree of Node)：结点所拥有的子树的个数，在图中，结点A的度为3 。
3、树的度(Degree of Tree)：树中各结点度的最大值 。在图5.1中，树的度为3 。
4、叶子结点(Leaf Node)：度为0的结点，也叫终端结点 。在图5.1中，结点E、F、G、H、I、J都是叶子结点 。
5、分支结点(Branch Node)：度不为0的结点，也叫非终端结点或内部结点 。在图5.1中，结点A、B、C、D是分支结点 。
6、孩子(Child)：结点子树的根 。在图中，结点B、C、D是结点A的孩子 。
7、双亲(Parent)：结点的上层结点叫该结点的双亲 。在图中，结点B、C、D的双亲是结点A 。
8、祖先(Ancestor)：从根到该结点所经分支上的所有结点 。在图中，结点E的祖先是A和B 。
9、子孙(Descendant)：以某结点为根的子树中的任一结点 。在图中，除A之外的所有结点都是A的子孙 。
什么是二叉树的度和深度二叉树结点的度数指该结点所含子树的个数 。
二叉树的深度是指所有结点中最深的结点所在的层数 。
二叉树上元素之间呈现什么关系

文章插图
树是一种重要的非线性数据结构，直观地看，它是数据元素按分支关系组织起来的结构，很象自然界中的树那样 。树结构在客观世界中广泛存在，如人类社会的族谱和各种社会组织机构都可用树形象表示 。
树在计算机领域中也得到广泛应用，如在编译源程序如下时，可用树表示源源程序如下的语法结构 。又如在数据库系统中，树型结构也是信息的重要组织形式之一 。一切具有层次关系的问题都可用树来描述 。满二叉树，完全二叉树，排序二叉树 。
在计算机科学中，二叉树是每个结点最多有两个子树的有序树 。通常子树的根被称作“左子树”和“右子树” 。二叉树常被用作二叉查找树和二叉堆或是二叉排序树 。
二叉树的数据结构描述了数据之间的哪种关系描述了数据元素之间的层次关系
二叉排序树操作详解二叉排序树（BinarySortTree，简称BST）又叫二叉查找树和二叉搜索树，是一种实现动态查找表的树形存储结构 。

推荐阅读


上一篇：野生蚂蟥怎么抓 「抓蚂蝗的最佳时间」

下一篇：月影多肉种类