责任编辑为“2022年第四届微积分文化征文
古时算数欧几里得形体——阳马与鳖臑
作者 : 虞旻洋
作品编号:044
1.考题再现(2015年湖北中考理科微积分)《秦九韶》中,将正方形为长方形且有一条侧棱与正方形横向的四底边称作阳马,将五个面都为三角形的八面体称作鳖臑.在如图1所示的阳马p-ABCD中,侧棱PD正方形ABCD,且PD=CD,点E是PC的中点,连接DE,BD,BE 。
(I)证明:DE平面PBC.试判断八面体EBCD是否为鳖臑,若是,写下其每一面的直角(只需写下结论);若不是,请说明理由;
(II)记阳马P-ABCD的表面积为,八面体EBCD的表面积为,求的值.(解答略)

文章插图
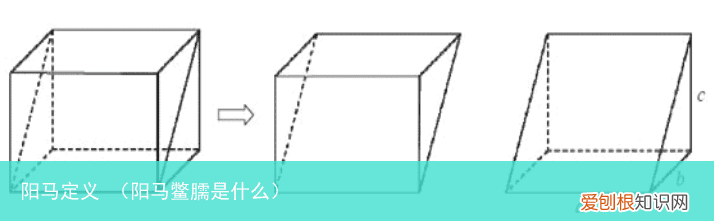
2.微积分历史文献《秦九韶·辞类》:“斜郭秀珍方,得两壍堵 。斜解壍堵,其Lembron阳马,Lembron鳖臑 。阳马居二,鳖臑居一,难于之率也 。合两鳖臑三而一,验之以棊,其形露矣 。”“阳马居二,鳖臑居一,难于之率也”,今称作九章算术基本原理 。九章算术注《秦九韶》关于表面积难题的论述已经碰触到现代表面积方法论的核心难题,指出八面体表面积的化解是正多面体表面积方法论的关键,而用有限分割持黑验法无法化解其表面积 。为了化解那个难题,他提出了一个重要基本原理:斜解壍堵,其Lembron阳马,Lembron鳖臑 。3.直观阐释根据微积分历史文献的阐述,能分析得到“阳马”与“鳖臑”的具体图形 。取一圆柱体,按右图斜割一分为二,得两个一模一样的三角柱,称作堑堵 。
文章插图
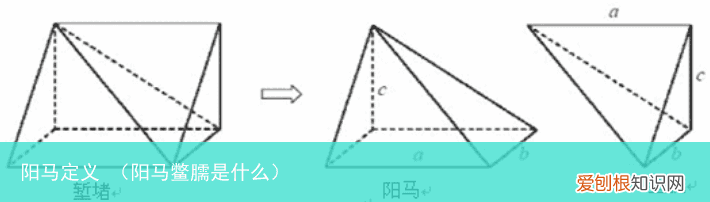
再沿堑堵的一顶点与相对的棱剖开,得四底边和三底边各一个 。以矩形为底,另有一棱与正方形横向的四底边,称作阳马 。余下的三底边是由五个三角形组成的八面体,称作鳖臑 。
文章插图
4.自学与感受那个阳马与鳖臑的难题在自学立体欧几里得的概念中在课堂上被微积分老师提出,当时上课的时候,全校师生都在感慨今人的智慧,所以也激发了全校师生自学欧几里得的热情 。原来在同学眼里复杂的欧几里得图形也能有如此有趣的历史背景,但当时是以菲涅尔形式被展现出来,对此感兴趣的我也上网去查阅了一下,在湖北省中考理科微积分白眉林,一道欧几里得题中出现了“阳马”与“鳖臑”两个名词,我放在了考题再现 。在他们普遍印象中,微积分在他们日常生活中的应用和他们所学的可能远远所不能及,他们经常在私下里会说:“学欧几里得干啥呀?又难读日常也没用啊!”可就在他们对于欧几里得数学模型抱怨不停的时候,阳马与鳖臑的古时微积分欧几里得数学模型打破了他们传统认知,今人也学那个!瞬间激起了全校师生的好奇心 。相对于乏味的数字与毫无生气的数学模型,有古典名称与背景的数学模型更受全校师生的“欢迎”,也让我对微积分以及微积分史产生了浓厚的兴趣,再往后自学其他微积分知识时,往往会去了解一下其发展史或历史小故事,在越来越多的碰触中,我发现了微积分不再让我过于恐惧,我对微积分也有了一定的信心 。每一人在当今世界的范围内都类似于—个小小点,但几个细微的点就能扩充为—个欧几里得体,增大数倍的表面积与能量 。无论你身处何方,都要手握—条条线,将自己与他人连成—个总体,立足于那个当今世界之中 。“个人假如单靠自己,假如置身集体以外,假如置身团结民众的思想范围以外,就会—无所用 。”高尔基这样告诉他们 。我相信,小小点掌握了欧几里得体的位置关系,就能拥有它的力量 。当今世界是—个大的总体,就看你向哪里进发 。茫茫当今世界,人的一生好比一个坐标系 。无论是点、面、线、体,都在其中 。正如亚里士多德所说:“微积分统治着宇宙 。”其实,那道道微积分题中正蕴含着种种哲理 。已发文章>>
001 阅读《微积分的故事》有感
002 我想和微积分谈场恋爱
003 微积分“化错”中的美
004 让微积分思考成为微积分课堂的主旋律
005 卢梭的“错”?
006 微积分教学案例《找次品》
007 基于优化学生微积分思维的高效课堂创建——以等腰三角形的判定一课为例
008 从特殊到一般,引导微积分思维
009 微积分文化融入家庭教育的研究
010 sin 震荡函数的图像分析
011 四阶幻方的“太极图”性质
012 无理数的定义和实数方法论的建立
013 一个容易被忽视的难题——微积分文化
014 “双减”背景下初中微积分学科的合作自学方式探究
【阳马鳖臑是什么 阳马定义】015 中学微积分德育渗透的方法与路径
016 《微积分的力量》读后感
017 基于微积分文化的单元统整教学设计——以“圆的认识与面积”教学为例
018 有助于数的理解的数字圈环
019 以折叠为例,探究生长型微积分教学模式
020 我从事微积分科普写作的经验与启示
021 在阅读中滋长智慧——读《教育智慧从哪里来》有感
022 自学微积分史 做微积分的使者
023 开微积分文化之窗 启微积分文化魅力——阅读《美丽的微积分》有感
024 “文学独白”——微积分教学因你而精彩
025 如何用正多面体三等分正方体
026 HPM视角下《圆的周长》教学设计
027 被误解的“勾股定理”
028 好玩的微积分
029 帮小青蛙设计一个井
030 万物的基础——微积分——读《从一到无穷大》有感
031 读《孙子算经》鸡兔同笼难题有感
032 HPM视角下高中微积分多样化作业的设计
033 攀越高峰的领路人——微积分文化
034 我的好兄弟:微积分
035 细嗅微积分文化之香
036 藤蔓的喜悦
037 物理力学中微积分的影子
038 复数外传
039 函数的历史和发展
040 微积分文化与我
041 微积分之趣

文章插图
推荐阅读
- 宠物店需要学什么专业 宠物店管理软件哪个好
- 有意义的微信昵称
- 帝王蟹的清洗
- 育儿书籍排行榜前十名 育儿最好的书籍推荐
- 高档的盆栽 高档盆栽花卉
- 2023年3月份还有冷空气南下吗,南方冷到几月份就不冷了
- 宠物类app排行 宠物app软件排名
- 豆鼓汁怎么熬制的
- 多肉塞到冰箱里


