两个难题:
「烫之后的三片地板为什么极难合二为一?」
这是两个非常众所周知的「貌似很单纯,只不过很繁杂」的难题 。
盛行的科学普及(甚至小学魏扶上)上似乎讲的很确切,但只不过真正的其原因并没讲明白 。
盛行科学普及上讲,虽然地板间充满著了水,它间没水蒸气,因此靠标准水蒸气压就能把它密切地抬升在一同 。如下表所示图右图:
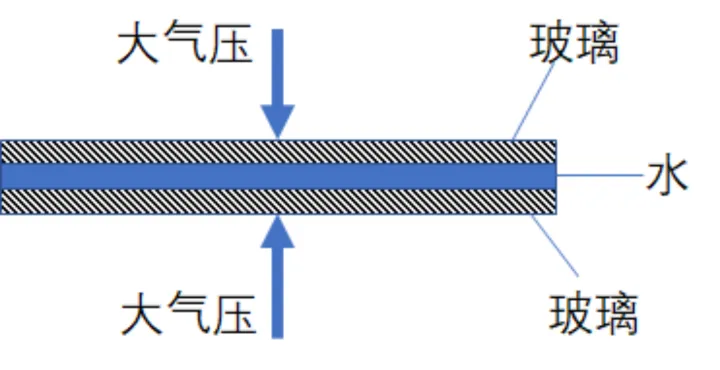
文章插图
但那个标准答案只不过并不恰当,换句话说并不精确 。
即使他们晓得,水也是满足用户欧姆基本原理的 。标准水蒸气压并更为重要是促进作用在地板表层的,地板尾端的水也与水蒸气有碰触,因此标准水蒸气压也会促进作用在空隙中的陆上的 。由欧姆基本原理,外间的标准压强是能透过水传达到地板间歇当中的 。
所以实际上是有水的充填,地板不能「被标准水蒸气压抬升在一同」 。他们能用下面的局部性弱化图来说明这种情况:
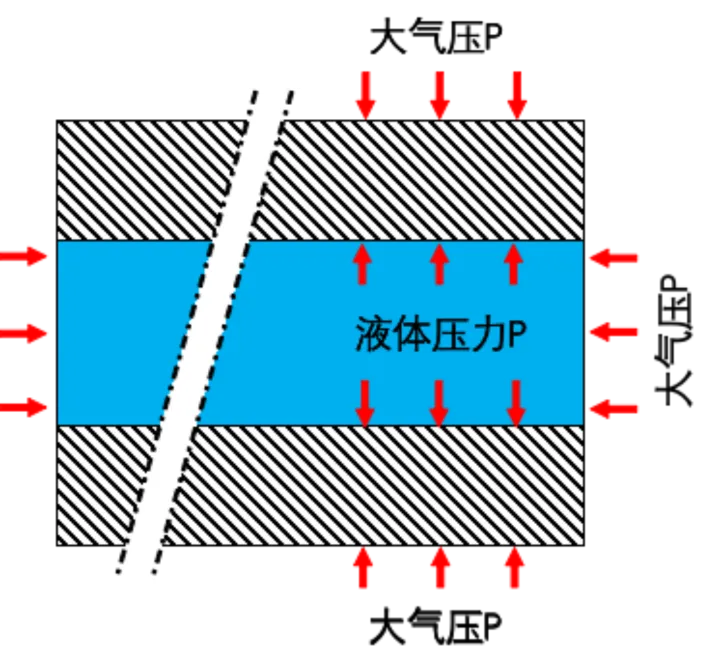
文章插图
换句话说,虽然欧姆基本原理,空隙中的水也会将标准水蒸气压传达到三片地板的空隙内部 。标准水蒸气压的促进作用效用绝非是「向内」抬升三片地板,即使在空隙内部同样存在着阻力 。
归根结底,固体和液体对标准水蒸气压的传达是完全相同的,因此纯粹从阻力的传达来说,地板片尾端有水还是没水并不能产生完全相同的效用 。
这里的真实世界其原因,只不过是粘滞与标准水蒸气压的协力促进作用 。
简而言之,下面的图稍稍有点儿严重错误:水和水蒸气的介面不是平的,而应该是两个凹冷却液 。而不可否认是那个凹冷却液,导致了完全完全相同的结果 。具体讲,就是使固体内部的阻力高于内部的标准压强 。
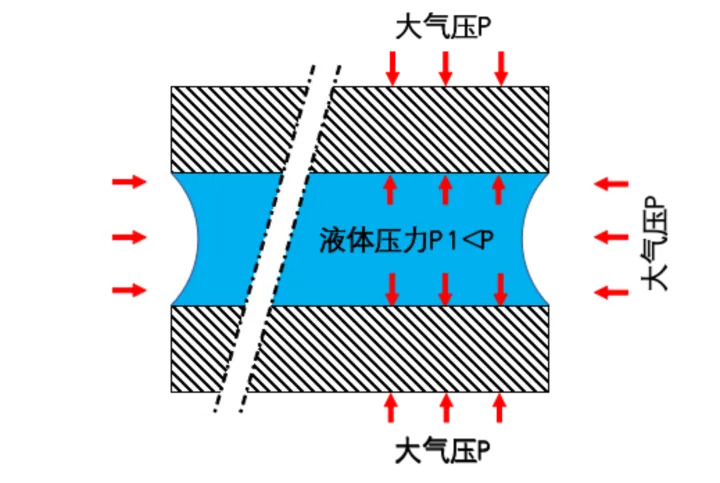
文章插图
而这里的罪魁祸首,就是粘滞 。
粘滞,他们单纯形象地理解,能认为流体的两相(如气液)介面就像是一张紧绷的皮膜,这张膜在外力的约束下,总是希望尽可能地收缩 。沿着它的表层就有一种张力,就是粘滞 。
如果你想用最形象的方式理解粘滞,你能想象两个吹起来的气球的表层:气球的弹力使它尽量收缩从而整体形成球形 。相对应地,水滴的粘滞使它尽量收缩从而形成球形 。

文章插图
而这里有一件非常关键的事请,就是虽然粘滞的存在,弯曲的表层就会在两侧形成阻力差 。
比如说,无重力液滴是两个球形 。他们对两个这样的液滴的上半球做两个受力分析,它受到三个力的促进作用:
1. 下半球在截面上对它的净阻力;
2. 内部在上半球面上对它的净阻力
3. 液滴表层受到的沿表层垂直于「断面」的粘滞 。
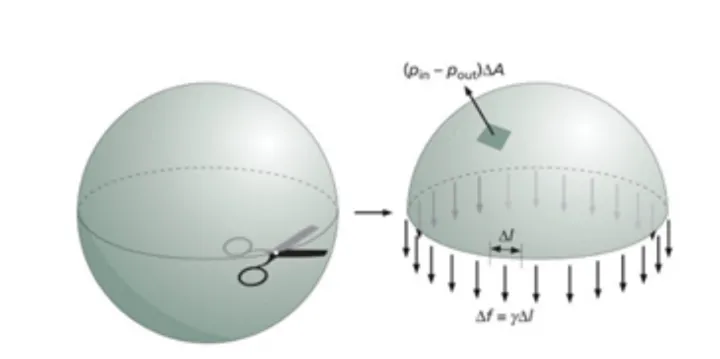
文章插图
他们很容易就会看到,虽然粘滞的存在,此时内部的阻力肯定要大于内部阻力 。只不过那个很容易理解:两个气球就是众所周知内部阻力大于内部阻力的例子,这种阻力差,就是有张力的皮膜形成的 。那么,这种阻力差的大小是由什么决定的呢?
很显然,两个决定因素就是张力的大小:皮膜绷的越紧,所能产生的阻力差就越大 。但还有另两个很重要的因素,就是表层弯曲的程度,也就是它的曲率 。他们还是用气球做两个说明,例如下表所示面那个气球:
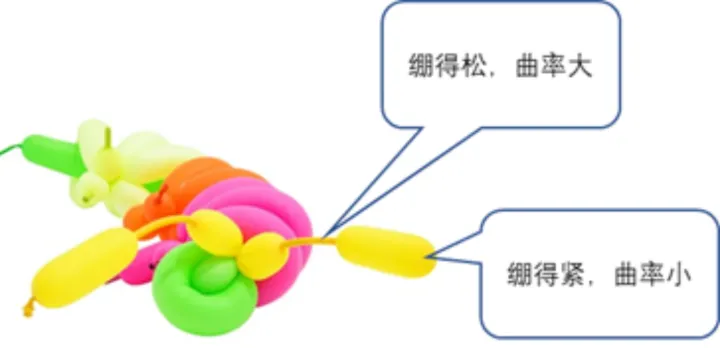
文章插图
气球内部的液体阻力处处相等,因此,气球内外的压差是两个常数 。但,碰触过这种气球的人都有两个经验,就是粗的地方绷得紧,而细的地方绷得就不那么紧 。换句话说,在起球完全相同的地方,皮膜的张力是完全相同的,如上图右图 。那么难题就来了,绷得紧的地方和绷得松的地方,产生的阻力差却是相等的,这是为什么?
其原因是,在绷得紧和绷得松的地方,皮膜的曲率是不相等的:曲率越大,同样的张力所能产生的阻力差就更大;曲率越小,同样的张力产生的阻力差就越小 。反过来说,如果产生同样的阻力差,曲率大的地方,所需要的张力就越小(在气球细的地方,皮膜就松) 。反之亦然(在气球粗的地方皮膜就紧) 。
他们有两个公式能表示那个关系,叫做杨-拉普拉斯方程(Young-Laplace equation):
其中,γ是粘滞,R1 和 R2 分别是两个方向上的曲率半径 。
现在,他们能来分析一下烫的地板为什么极难合二为一了 。
首先,他们晓得,固体与固体介面相碰触,都会形成两个碰触角 。碰触角也是粘滞的性质之一,这里我就不展开说了 。碰触角小于 90°的,被称作浸润(如水对地板就是浸润的),大于 90°的,叫做不浸润(如水银对地板就是不浸润的) 。
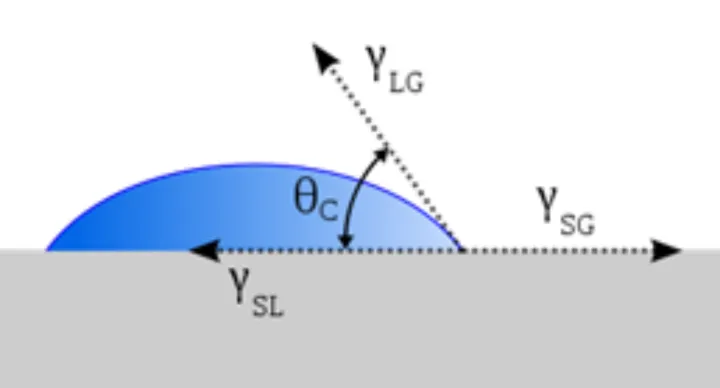
文章插图
在三片地板间,形成的凹冷却液就是即使那个碰触角的其原因:
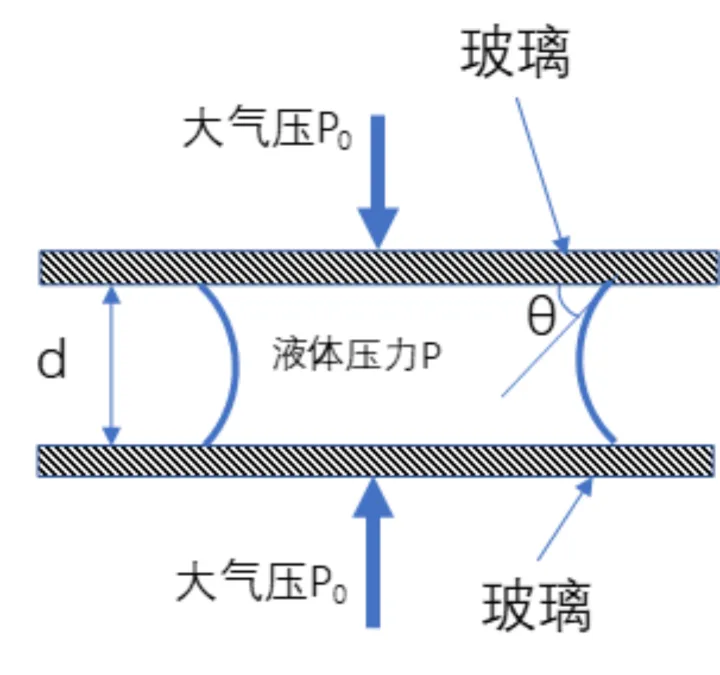
文章插图
他们看到,那个凹冷却液就形成了两个「反向」的紧绷的膜 。就像是气球两个道理,这种曲面的膜,虽然粘滞的其原因,就会使固体的阻力 P 小于内部标准水蒸气压 P0 。因此把地板抬升在一同的力,就不是 P0 而是 P0-P 。
他们能想象,当三片地板间歇非常小的时候,那个凹冷却液的曲率就会非常大,在那个时候,固体阻力与标准水蒸气压的差就会很大,因此把地板抬升在一同的力也就很大 。他们能用杨-拉普拉斯公式来估算一下 。
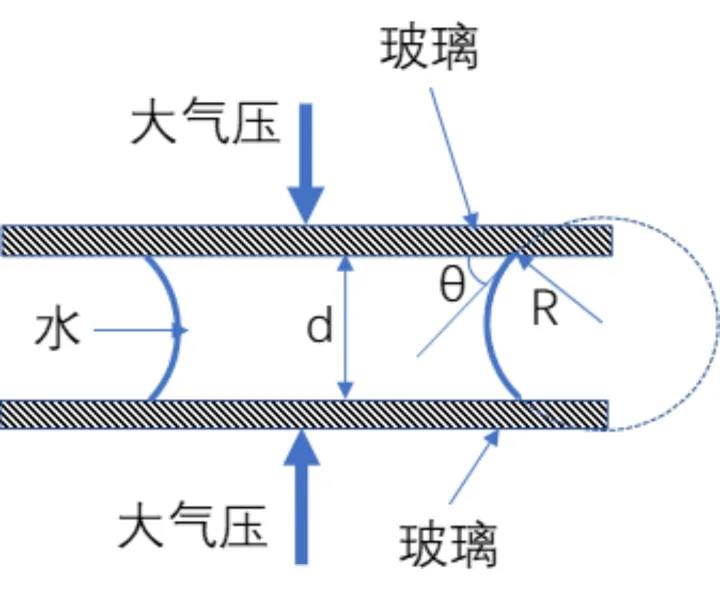
文章插图
那个凹冷却液沿着他们切面的视角上的曲率半径是(假设地板的间歇为 d):
因此,根据杨-拉普拉斯方程(他们假设液膜面积尺度远大于间歇尺度),那个凹冷却液所产生的固体内部与水蒸气间的阻力差为:
请注意,这里形成的阻力差是负值 。
已知他们做能做的最好的地板面,其表层粗糙度仅有纳米级 。而普通地板,也只有零点几到零点零几微米的尺度 。因此三片地板间的空隙,显然不是由粗糙度决定的 。
对于面积比较小的地板(翘曲忽略不计),这里考虑的是表层清洁度:换句话说,虽然地板表层的污渍存在,会使三片地板表层不能严密贴合 。一般 10 微米以上的灰尘他们肉眼都是能看见的,而在这之下就极难看到,2 微米之下就无法看到了 。所以我这里假设他们一般对地板表层清洁会留有 10 微米基本的污渍,换句话说,三片(面积不大的)地板的空隙数量级在 5 微米左右 。
常温下水的粘滞大约为 0.073N/m 。水在普通地板上的碰触角大约为 30°左右 。因此,对于贴合较好的三片地板片,很容易计算出那个液膜内部的阻力与标准水蒸气压的阻力差为 25Kpa – 大约为标准水蒸气压的 1/4 左右 。
换句话说,液膜内部阻力比标准水蒸气压小 25Kpa 。对于这样 10cm2 的三片地板,如果他们用一点水把它「沾」在一同,他们需要大约 250N 的力才能掰开 – 虽然极难,但如果有抓手的话还是有可能的 。
但如果是按照盛行科学普及的说法(液膜排出水蒸气导致地板间歇阻力为零),他们所需要 1000N 的力才能掰开,那个就不太可能了 。
他们能做两个实验,来验证那个解释 。我做了这样两个动图:

文章插图
他们能看到,三片地板被水沾在一同后,还是相当牢固的 。

文章插图
但当他们向着地板空隙滴几滴水,哪怕只是很少的几滴,它间就不再牢固了,随着水的不断滴入,最后就不可避免地合二为一了 。这是即使滴入水不断进入空隙,最后就会破坏掉前面所述的曲率很大的冷却液,导致固体阻力与外间气压的差迅速降低,于是它就无法继续沾在一同了 。那个过程能图示如下表所示:
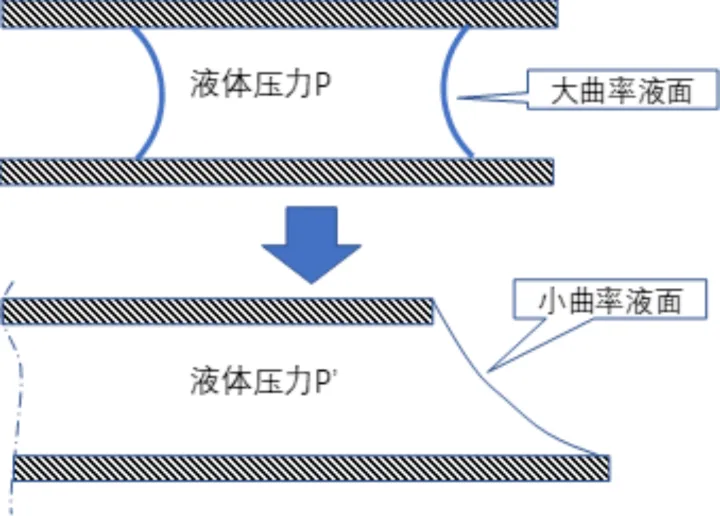
文章插图
【你知道的生活小常识有哪些英语作文,你知道的生活小常识有哪些?】?所以说,纯粹从「固体占据了空隙因此内部没液体」并不能解释地板为什么能沾在一同 。这里面粘滞以及其引发的阻力差(杨-拉普拉斯方程)才是关键因素 。
推荐阅读
- 奇奕画王怎么用
- 《圆明园的毁灭》读后感作文350字
- 洛克王国作文150字
- 更新ing 宠物知识大全整理,宠物小常识
- 芙蓉李子什么时候成熟
- 读《青铜葵花》有感作文700字
- qq空间描述短句子霸气
- 香奈儿42和43哪个更赞
- 养花有哪些技巧,这3个养花技巧,1分钟就能学会,轻轻松松养活1000盆花


