是质数也是合数，既是质数也是合数对吗

1是质数也是合数吗
1既不是质数也不是合数。
质数是指在大于1的自然数中，除了1和它本身以外不再有其他因数的自然数。质数又称素数。一个大于1的自然数，除了1和它自身外，不能被其他自然数整除的数叫做质数。
合数是指在大于1的整数中除了能被1和本身整除外，还能被其他数（0除外）整除的数。与之相对的是质数，而1既不属于质数也不属于合数。最小的合数是4 。其中，完全数与相亲数是以它为基础的。
既是质数也是合数对吗合数是指在大于1的整数中除了能被1和本身整除外，还能被其他数（0除外）整除的数。
与之相对的是质数，而1既不属于质数也不属于合数。最小的合数是4 。其中，完全数与相亲数是以它为基础的。
合数可分为奇合数和偶合数，也能基本合数（能被2或3整除的），分阴性合数（6N-1）和阳性合数（6N+1），还能分双因子合数和多因子合数。

文章插图
扩展资料：
性质
1、所有大于2的偶数都是合数。
2、所有大于5的奇数中，个位为5的都是合数。
3、除0以外，所有个位为0的自然数都是合数。
4、所有个位为4 ， 6 ， 8的自然数都是合数。
5、最小的（偶）合数为4 ，最小的奇合数为9 。
6、每一个合数都可以以唯一形式被写成质数的乘积，即分解质因数。(算术基本定理)
0是质数还是合数1既不是质数也不是合数。
解析如下：
如果1是质数，那它就要有两个因数：1=1×1
如果1是合数，那它就要有三个及以上的因数：1×1×1×1??
化简之后就是1=1 ，只有一个因数，因此， 1既不是质数也不是合数。

文章插图
扩展资料：
只有1和它本身两个因数的自然数，叫质数（或称素数）。（如：由2÷1=2 ， 2÷2=1 ，可知2的因数只有1和它本身2这两个因数，所以2就是质数。
与之相对立的是合数：“除了1和它本身两个因数外，还有其它因数的数，叫合数。”如：4÷1=4 ， 4÷2=2 ， 4÷4=1 ，很显然， 4的因数除了1和它本身4这两个因数以外，还有因数2 ，所以4是合数。）
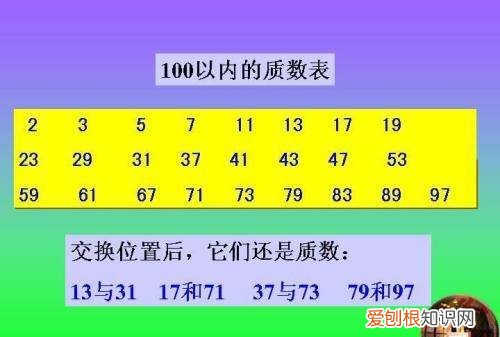
100以内的质数有2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53、59、61、67、71、73、79、83、89、97 ，一共有25个。
质数的个数是无穷的。欧几里得的《几何原本》中的证明使用了证明常用的方法：反证法。具体证明如下：假设质数只有有限的n个，从小到大依次排列为p1 ， p2 ， ?? ， pn ，设N=p1×p2×??×pn ，那么， N+1是素数或者不是素数。
如果N+1为素数，则N+1要大于p1 ， p2 ， ?? ， pn ，所以它不在那些假设的素数集合中。
如果N+1为合数，因为任何一个合数都可以分解为几个素数的积；而N和N+1的最大公约数是1 ，所以N+1不可能被p1 ， p2 ， ?? ， pn整除，所以该合数分解得到的素因数肯定不在假设的素数集合中。
因此无论该数是素数还是合数，都意味着在假设的有限个素数之外还存在着其他素数。所以原先的假设不成立。也就是说，素数有无穷多个。

是质数也是合数，既是质数也是合数对吗

推荐阅读

关于节约粮食的名言诗句关于节约粮食的名言和诗句

奋斗励志朋友圈句子励志短句致自己奋斗朋友圈

想发朋友圈表示心情不好的句子心情不好发朋友圈的句子心情短句

贝拉玻尿酸是合法的吗贝拉玻尿酸是进口的还是国产的

核桃仁做菜的菜谱，您知道桃仁脆溜鸡的做法

浅紫色显皮肤黑还是白

库伦旗景点

居家隔离和集中隔离的区别什么情况下要隔离28天

蝉蛹是什么

怎样能丰胸最安全有效