小于Q1-1.5(IQR)或者大于Q3+1.5(IQR);
对于异常值,我们在数据处理的环节就要剔除;
4.方差
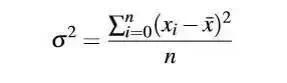
文章插图
5.平方偏差
方差的算术平方根
6.贝塞尔矫正:修正样本方差
实际在计算方差时,分母要用n-1,而不是样本数量n 。原因在于,比如在高斯分布中,我们抽取一部分的样本,用样本的方差表示满足高斯分布的大样本数据集的方差 。由于样本主要是落在x=u中心值附近,那么样本如果用如下公式算方差,那么预测方差一定小于大数据集的方差(因为高斯分布的边沿抽取的数据也很少) 。为了能弥补这方面的缺陷,那么我们把公式的n改为n-1,以此来提高方差的数值,这种方法叫贝塞尔矫正系数 。
三、归一化
1.标准分数
一个给定分数 距离 平均数 多少个标准差?
标准分数是一种可以看出某分数在分布中相对位置的方法 。
标准分数能够真实的反映一个分数距离平均数的相对标准距离 。
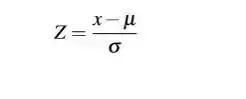
文章插图
四、正态分布
1.定义:随机变量X服从一个数学期望为μ,方差为σ?2;的正态分布,记为N(μ,σ?2;)
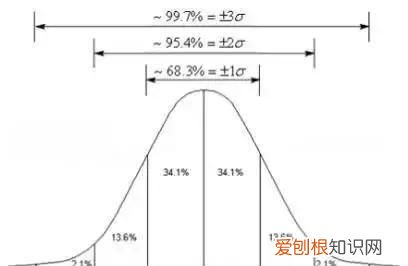
随机取一个样本,有68.3%的概率位于距离均值μ有1个标准差σ内;
有95.4%的概率位于距离均值μ有2个标准差σ内;
有99.7%的概率位于距离均值μ有3个标准差σ内;
文章插图
五、抽样分布
1.中心极限定理
设从均值为μ,方差为σ?2;的任意一个总体中抽取样本量为n的样本,当n充分大时,样本均值的抽样分布近似服从均值为μ、方差为σ?2;/n的正态分布
2.抽样分布
设总体共有N个元素,从中随机抽取一个容量为n的样本,在重置抽样时,共有N·n种抽法,即可以组成N·n不同的样本,在不重复抽样时,共有N·n个可能的样本 。每一个样本都可以计算出一个均值,这些所有可能的抽样均值形成的分布就是样本均值的分布 。但现实中不可能将所有的样本都抽取出来,因此,样本均值的概率分布实际上是一种理论分布 。数理统计学的相关定理已经证明:在重置抽样时,样本均值的方差为总体方差的1/n 。
举个例子:
48盆MM豆,计算出每盆有几个蓝色的MM豆,48个数据构成了总体样本 。然后随机选择五盆,计算五盆中含有蓝色MM豆的平均数,然后反复进行了50次 。这就是n为5的样本均值抽样 。
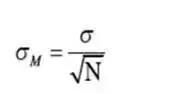
文章插图
六、估计
1. 误差界限
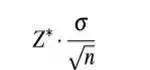
文章插图
2. 置信度
We are some % sure the true population parameter falls within a specific range
我们有百分之多少确信总体中的值落在一个特定范围内;
一般情况下,取95%的置信度就可以;
3. 置信区间
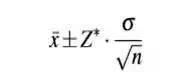
文章插图
七、假设检验

文章插图
1.问题:什么是显著性水平?
显著性水平是估计总体参数落在某一区间内,可能犯错误的概率,也就是Type I Error
A Type II Error is when you fail to reject the null when it is actually false.

文章插图
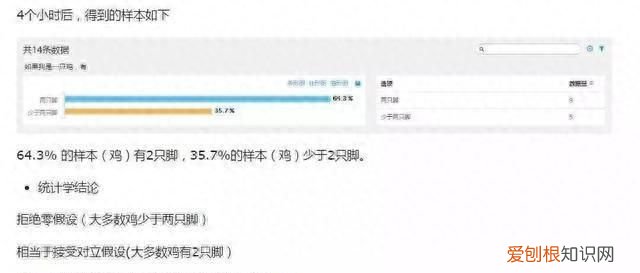
文章插图
2. 如何选择备选检验和零假设?
一个研究者想证明自己的研究结论是正确的,备择假设的方向就要与想要证明其正确性的方向一致;
推荐阅读
- eve lom急救面膜祛痘吗 eve lom面膜怎么样
- T-Mobile首席执行官暗示本周将发布新的非运营商声明
- 护手霜晚上可以用吗 护手霜晚上睡觉可以用吗
- 网店详情页怎么做 淘宝详情页面怎么制作
- 鼻子长痘什么健康问题 鼻子长痘是
- Onecom宣布收购Glamorgan Telecom Group
- 多尔衮和皇太极的关系怎么样 皇太极和多尔衮谁更有能力
- 匹克攀登者联名发售时间
- 怎么判断美妆蛋质量好不好


